3.2.46 #
解答 #
翻译有些问题,其实指的是用 N 个 double 构造一个 BST 和 BinarySearchST 的速度对比。
Get 速度 BST 是不会比 BinarySearchST 快的。($1.39\lg N$>$\lg N$)
二叉搜索树一次查找平均需要 $1.39\lg N$ 次比较,二分查找则是 $N/2$,于是可以求得开销:
二叉查找树:$1.39 \sum_{i=1}^{N-1} \lg i=1.39 \lg (N-1)!=1.39(N-1)\lg(N-1)$。
二分查找实现的符号表:$1/2+2/2+ \cdots+(N-1)/2=N(N-1)/4$ 。
令两式相等,可以求得快 10 倍,100 倍,1000 倍的 $N$ 值。 例如快 10 倍的方程:
$$ 13.9(N-1)\lg(N-1)=N(N-1)/4 \newline 13.9\lg (N-1)=N/4 $$
这是一个超越方程,可以简单用程序穷举出一个数值解。
for (var i = 0d; i < int.MaxValue; i++)
{
if (13.9 * Math.Log2(i - 1) < i / 4)
{
Console.WriteLine(i);
return;
}
}
解得的三个 N 值分别为 499,7115,91651。
除了基本的新元素赋值外,二叉树在插入时只需要进行比较即可。
但二分查找实现的符号表还需要维持数组有序,需要额外的赋值操作。
因此二分查找实现的符号表和二叉搜索树的开销如下:
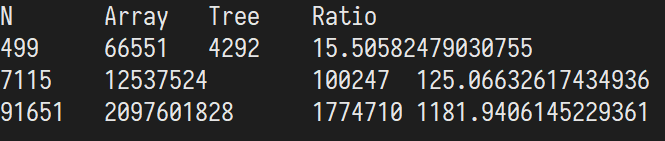
其中 Array 包含了比较和额外的赋值次数,Tree 只有比较次数。
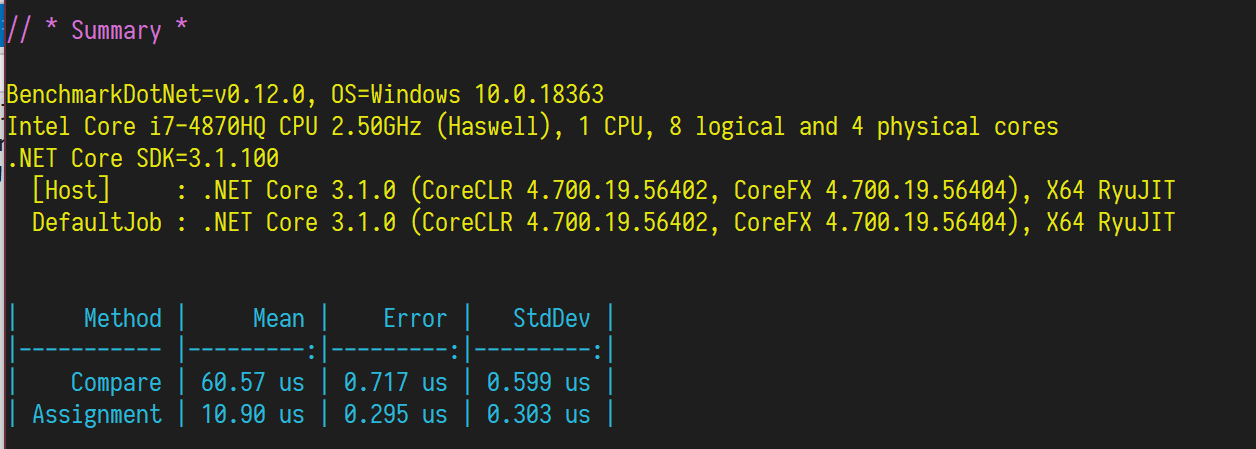
一般我们认为比较(Compare)和赋值(=)开销是一样的,但实际上比较会慢 6 倍左右(.net core 3.1),因此如果直接进行计时测试,可能得不出快 10 倍/100 倍/1000 倍的结果。