3.2.40 #
解答 #
书中的结论是 1986 年 L. Devroye 给出的,原式为 $H_n \rightarrow c\log(n)$。
其中 $c$ 是方程 $c\log \frac{2e}{c}=1$ 的最大解,约为 $4.31107$。
2002 年 Michael Drmota 给出了一个跟精确的公式:$\mathrm{E}(H_n)=c\log n-\frac{3c}{2(c-1)}\log \log n + O(1)$。
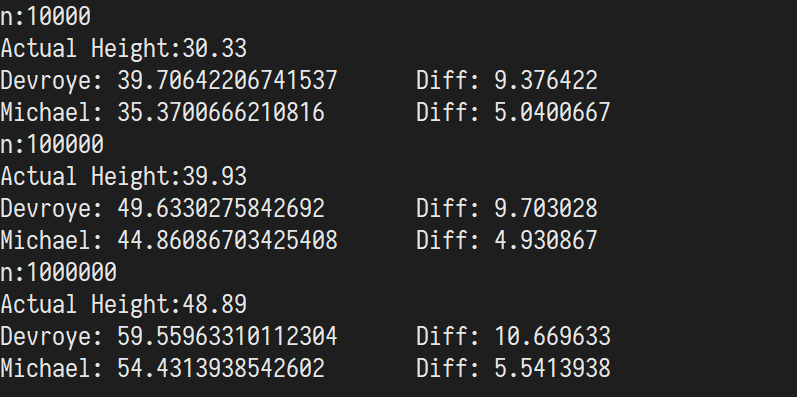
测试结果如下,误差基本稳定在一个常数。
代码 #
static void Main(string[] args)
{
var n = 10000;
var trials = 100;
for (var i = 0; i < 3; i++)
{
var items = new int[n];
for (var j = 0; j < n; j++)
{
items[j] = j;
}
var aveHeight = 0d;
for (var j = 0; j < trials; j++)
{
var bst = new BST<int, int>();
Shuffle(items);
foreach (var item in items)
{
bst.Put(item, item);
}
aveHeight += bst.Height();
}
aveHeight /= trials;
var c = 4.31107d;
var expectHeightLuc = c * Math.Log(n);
var expectHeightMichael = c * Math.Log(n) - (3 * c / (2 * (c - 1))) * Math.Log(Math.Log(n));
Console.WriteLine("n:" + n);
Console.WriteLine("Actual Height:" + aveHeight);
Console.WriteLine("Devroye: " + expectHeightLuc + "\tDiff: " + (float)(expectHeightLuc - aveHeight));
Console.WriteLine("Michael: " + expectHeightMichael + "\tDiff: " + (float)(expectHeightMichael - aveHeight));
n *= 10;
}
}
static void Shuffle<T>(T[] a)
{
var random = new Random();
for (var i = 0; i < a.Length; i++)
{
var r = i + random.Next(a.Length - i);
var temp = a[i];
a[i] = a[r];
a[r] = temp;
}
}
另请参阅 #
A note on the height of binary search tree