3.1.34 #
解答 #
在上一题的基础上进行修改即可。
调和级数 $H_n = 1+\frac{1}{2}+\frac{1}{3} + \cdots+\frac{1}{n}$ 。
查询数组变为前 1/2 为 key[0],随后的 1/3 为 key[1],以此类推。
和上一题中的序列进行比较即可,注意删除最后的打乱步骤。
实验结果如下:
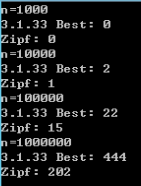
代码 #
首先建立一个数组计算调和级数,就像这样:
// 调和级数
var harmonicNumber = new double[n * (int)Math.Pow(10, multiplyBy10)];
harmonicNumber[0] = 1;
for (var i = 1; i < harmonicNumber.Length; i++)
{
harmonicNumber[i] = harmonicNumber[i - 1] + 1 / (i + 1);
}
然后修改构造查询的代码:
// 构造查询
Array.Sort(keys);
var queryZipf = new string[10 * n];
int queryIndex = 0, keyIndex = 0;
while (queryIndex < queryZipf.Length)
{
var searchTimes = (int)Math.Ceiling(queryZipf.Length / (harmonicNumber[keyIndex + 1] * (i + 1)));
for (var j = 0; j < searchTimes && queryIndex < queryZipf.Length; j++)
{
queryZipf[queryIndex++] = keys[keyIndex];
}
keyIndex++;
}