3.1.27 #
解答 #
事实上就是说,先构造一个包含 N 个不重复键的符号表,然后进行 S 次查找。
给出 S 的增长数量级,使得构造符号表的成本和查找的成本相同。
这里假设一次数组交换和一次比较的成本是相同的。
先考虑构造符号表的成本,一次 Put() 需要调用一次 Rank() 和一次插入操作。
2.1 节插入排序的命题 B 给出了每次插入平均需要移动一半的数组元素的结论。
于是构造符号表所需的成本约为:$n\lg n + \frac{1}{2}\sum_{k=1}^{n} k=n\lg n + \frac{n(n-1)}{4} $ 。
这里查找的成本是这么计算的:$\lg0+\lg1+\cdots+\lg n < n\lg n$
查找所需的成本比较简单,一次二分查找的比较次数约为 $\lg n$,总成本就是 $S\lg n$ 。
令两边相等,解方程即可得到 $S=n+\frac{n(n-1)}{4\lg n}$ 。
如果用大 O 记法,也可以记为 $O(n^2 / \lg n)$,如果要选择一个比较常用的上界则可以选择 $O(n^2)$。
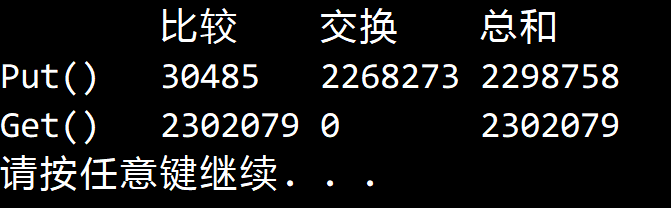
实验结果,两边的成本是很接近的: