3.1.24 #
解答 #
FrequencyCounter 的官方实现:https://algs4.cs.princeton.edu/31elementary/FrequencyCounter.java.html
二分查找总是与中间值进行比较,现在改为与数组中第 x% 位置上的元素比较。
具体而言,$\frac{k_x-k_{lo}}{k_{hi}-k_{lo}}$ 代表数组在均匀情况下目标值 $k_x$ 的相对位置(一个比率,在数组第 x% 的位置上)。
那么相对应的下标就等于 $lo+\frac{k_x-k_{lo}}{k_{hi}-k_{lo}} \times (hi - lo)$。
用这个式子代替原来的 $mid=lo + (hi-lo)/2$ 即可。
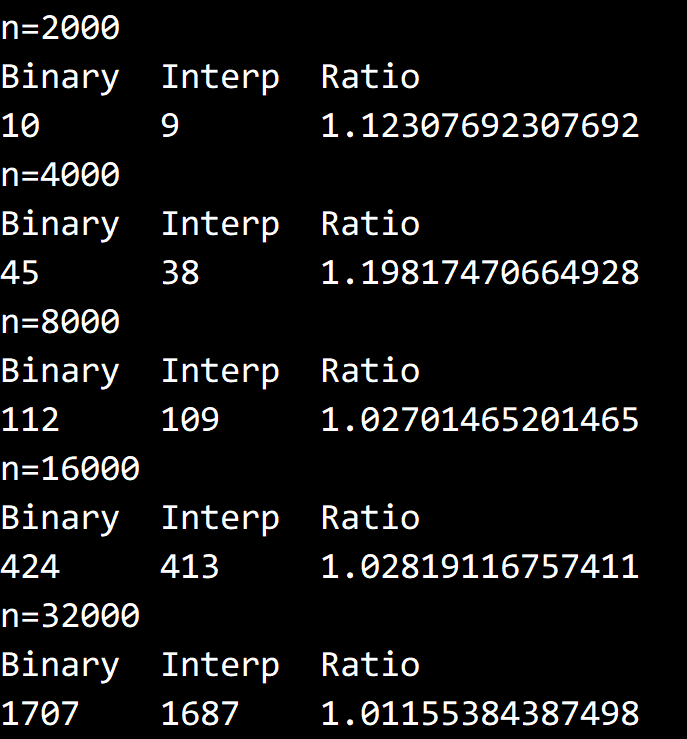
不难看出这种方法对于分布相对均匀的数组比较有利,相对于二分查找而言迭代次数会少很多。
但如果数组分布不够均匀,也可能表现出不如二分查找的性能。
实验结果也证实了这一判断,就随机数组而言,插值查找相对于二分查找只有 1% 左右的性能提升。
代码 #
SearchCompare 在书中没有出现,但可以简单的实现为调用 FrequencyCounter 并计时的方法:
public static long Time<TKey>(IST<TKey, int> st, TKey[] keys)
{
Stopwatch sw = new Stopwatch();
sw.Start();
FrequencyCounter.MostFrequentlyKey(st, keys);
sw.Stop();
return sw.ElapsedMilliseconds;
}
由于这里需要使用数字而非字符串作为键值,需要对官方给出的 FrequencyCounter 做一些修改:
public static TKey MostFrequentlyKey<TKey> (IST<TKey, int> st, TKey[] keys)
{
foreach (TKey s in keys)
{
if (st.Contains(s))
st.Put(s, st.Get(s) + 1);
else
st.Put(s, 1);
}
TKey max = keys[0];
foreach (TKey s in st.Keys())
if (st.Get(s) > st.Get(max))
max = s;
return max;
}