2.5.7 #
解答 #
参考书中给出的快速排序性能分析方法(中文版 P186,英文版 P293)。
设 $C_n$ 代表找出 $n$ 个元素中的最小值所需要的比较次数。
一次切分需要 $n+1$ 次比较,下一侧的元素个数从 $0$ 到 $ n-1 $ 都有可能,
于是根据全概率公式,有:
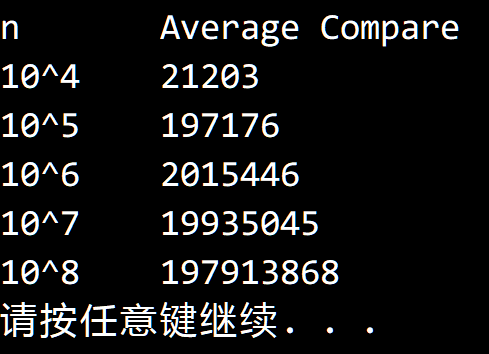
$$ \begin{eqnarray} C_n&=&\frac {1}{n} (n+1) +\frac{1}{n} (n+1+C_1)+ \cdots + \frac{1}{n}(n+1+C_{n-1}) \newline C_n&=&n+1+\frac{1}{n}(C_1+C_2+\cdots+C_{n-1}) \newline nC_n&=&n(n+1)+(C_1+C_2+\cdots+C_{n-1}) \newline nC_n-(n-1)C_{n-1}&=&2n+C_{n-1} \newline nC_n&=&2n+nC_{n-1} \newline C_n&=&2+C_{n-1} \newline C_n &=& C_1+2(n-1) \newline C_n &=& 2n-2 < 2n \end{eqnarray} $$
测试结果符合我们的预期。
附加:找出第 $k$ 小的数平均需要的比较次数。
类似的方法也在计算快速排序的平均比较次数时使用,见 {% post_link 2-3-14.md %}。
首先和快速排序类似,select 方法的所有元素比较都发生在切分过程中。
接下来考虑第 $i$ 小和第 $j$ 小的元素($x_i$ ,$x_j$),
当枢轴选为 $x_i$ 或 $x_j$ 时,它们会发生比较;
如果枢轴选为 $x_i$ 和 $x_j$ 之间的元素,那么它们会被切分到两侧,不可能发生比较;
如果枢轴选为小于 $x_i$ 或大于 $x_j$ 的元素,它们会被切分到同一侧,进入下次切分。
但要注意的是,select 只会对切分的一侧进行再切分,另一侧会被抛弃(快速排序则是两侧都会再切分)。
因此我们需要将第 $k$ 小的数 $x_k$ 纳入考虑。
如果 $x_k>x_j>x_i$ ,且枢轴选了 $x_k$ 到 $x_j$ 之间的元素,切分后 $x_i$ 和 $x_j$ 会被一起抛弃,不发生比较。
如果 $x_j > x_k > x_i$ ,枢轴的选择情况和快速排序一致。
如果 $x_j > x_i > x_k$ ,且枢轴选了 $x_i$ 到 $x_k$ 之间的元素,切分后 $x_i$ 和 $x_j$ 会被一起抛弃,不发生比较。
综上我们可以得到 $x_i$ 和 $x_j$ 之间发生比较的概率 $\frac{2}{\max(j-i+1, k-i+1,j-k+1)}$ 。
我们利用线性规划的知识把最大值函数的区域画出来,如下图所示:

对蓝色区域积分得:
$$ \begin{eqnarray} &&\int_{0}^{k} dj \int_{0}^{j} \frac{2}{j-k+1}\ di \newline &=& 2 \int_{0}^{k} \frac{j}{j-k+1} \ dj \newline &<& 2 k \end{eqnarray} $$
对红色区域积分得:
$$ \begin {eqnarray} && \int_{k}^{n} di \int_{i}^{n} \frac{2}{k-i+1} dj \newline &=& 2\int_{k}^{n} \frac{n-i}{k-i+1} di \newline &<& 2(n-k) \end {eqnarray} $$
对绿色区域积分得:
$$ \begin{eqnarray} && \int_{0}^{k}di\int_{k}^{n} \frac{2}{j-i+1} dj \newline &<& \int_{0}^{k}di\int_{k}^{n} \frac{2}{j-i} dj \newline &=& 2\int_{0}^{k} \ln (n-i) di - 2\int_{0}^{k} \ln(k-i)di \newline &=& 2i\ln(n-i) \bigg|{0}^{k} + 2\int{0}^{k}\frac{i}{n-i} di - \left[ i\ln(k-i) \bigg|{0}^{k} + 2\int{0}^{k} \frac{i}{k-i} di \right] \newline &=& 2k\ln(n-k)+2\int_{0}^{k}\frac{n}{n-i}-1 \ di -2\int_{0}^{k} \frac{k}{k-i}-1 \ di \newline &=& 2k\ln(n-k)+2\int_{0}^{k}\frac{n}{n-i} \ di -2k - 2\int_{0}^{k} \frac{k}{k-i} \ di +2k \newline &=& 2k\ln(n-k) -2n\ln(n-i) \bigg|{0}^{k} +2k\ln(k-i)\bigg|{0}^{k} \newline &=& 2k\ln(n-k)-2n\ln(n-k)+2n\ln n -2k\ln k \end{eqnarray} $$
全部相加得到:
$$ \begin{eqnarray} && 2k+2(n-k)+2k\ln(n-k)-2n\ln(n-k)+2n\ln n -2k\ln k \newline &=& 2n + 2k\ln(n-k)-2n\ln(n-k)+2n\ln n -2k\ln k \newline &=& 2n + 2k\ln(n-k)-2n\ln(n-k)+2n\ln n-2k\ln k +2k\ln n-2k\ln n \newline &=& 2n + 2k\ln n-2k\ln k+2n\ln n-2n\ln(n-k) - 2k\ln n + 2k\ln(n-k) \newline &=& 2n + 2k\ln \left(\frac{n}{k} \right)+2n\ln\left(\frac{n}{n-k} \right) - 2k\ln\left(\frac{n}{n-k} \right) \newline &=& 2n+2k\ln\left(\frac{n}{k}\right)+2(n-k)\ln\left(\frac{n}{n-k} \right) \end{eqnarray} $$
于是得到了命题 U 中的结果(中文版 P221,英文版 P347)。