2.5.32 #
解答 #
(前置知识:提前了解 Dijkstra 算法能够降低理解 A* 算法的难度。)
A* 算法是 Dijkstra 算法和最佳优先算法的一种结合。
Dijkstra 算法需要遍历所有结点来找到最短路径,唯一的优化条件就是路径长度。
建立队列 queue ,把所有的结点加入 queue 中;建立数组 d,d[v] 代表起点到点 v 的距离。
开始时只有起点到起点的距离为 0,其他都为无穷大,然后重复如下步骤:
从队列中取出已知距离最短的结点 u,检查该结点的所有边。
如果通过这个点能够以更近的距离到达 v,更新起点到 v 的距离 d[v] = d[u] + distance(u, v)。
等到队列为空之后数组 d 中就存放着起点到其他所有结点的最短距离。
Dijkstra 算法会计算起点到所有点的最短路径,因此会均匀的遍历所有结点,效率较低。
很多时候,我们只需要找到起点到某一终点的最短路径即可,为此遍历整个图显然是不必要的。
通过修改算法,使得比较接近终点的结点优先得到搜索,我们就可能在遍历完全部结点之前获得结果。
在 Dijkstra 算法中,离起点最近的点会被优先搜索,记结点离起点的距离为 g[n] 。
现在引入新的条件,用于估计结点和终点的接近程度,记结点离终点的估计距离为 h[n] 。
令 f[n] = g[n] + h[n],我们按照 f[n] 对等待搜索的结点进行排序。
同时令 h[n] 始终小于 g[n] ,保证离起点的距离 g[n] 权重大于离终点的估计距离 h[n] 。
(h[n]也被称之为容许估计)
于是在离起点距离接近的条件下,离终点比较近的点会被优先搜索,减少搜索范围。
接下来就是算法的具体内容,与 Dijkstra 算法不同,A* 算法不一定需要访问所有结点,
因此 A* 算法需要维护两个集合,openSet 保存等待搜索的结点,closeSet 保存已经搜索过的结点。
和 Dijkstra 算法类似,一开始 openSet 中只有起点,closeSet 则是空的。
然后重复执行如下步骤,直到 openSet 为空:
从 openSet 中取出 f[n] 最小的结点 u ,放入 closeSet。(标记为已访问)
如果 u 就是终点,算法结束。
计算结点 u 直接可达的周围结点,放入集合 neighbors。
遍历 `neighbors` 中的所有结点 `v`,做如下判断:
如果 `v` 已经存在于 `closeSet` ,忽略之。(防止走回头路)
如果经过 `u` 不能缩短起点到 `v` 的路径长度 `g[v]`,忽略之。(和 Dijkstra 算法一样的做法)
否则将 `v` 放入 `openSet`,更新 `g[v] = g[u] + distance(u, v)` ,计算 `f[v] = g[v] + h[v]`。(更新结点)
以上是 A* 算法的核心逻辑,
为了结合具体问题,我们需要自定义计算 g[n] 和 h[n] 的方法,以及获得某个结点周围结点的方法。
这里有个问题,openSet 和 closeSet 应该用什么数据结构?
closeSet 比较简单,只需要添加和查找即可,哈希表 HashSet 是不二选择。
openSet 需要读取并删除最小元素,以及添加和查找元素,用最小堆 MinPQ 会是比较方便的方法。
书中给出的最小堆 MinPQ 没有实现 Contains 方法,需要自己实现一个,简单顺序查找就够用了。
同时 MinPQ 的 Greater 比较方法也需要重新实现,需要使用基于 f[n] 进行比较的比较器。
现在我们考虑 8 字谜题如何用 A* 算法实现。
棋盘的每一个状态就是一个结点,每走一步就能进入下一个状态,结点可以这么定义:
class SearchNode
{
int[] Board; // 棋盘状态
int Steps; // 已经使用的步数
}
g(start, goal) 直接就是 goal.Steps - start.Steps,h(start, goal) 则根据题意有不同的实现。
获得周围结点的方法 GetNeighbors(current),会返回一个数组,其中有从 current 上下左右走获得的棋盘状态。
运行结果,初始状态为:
0 1 3
4 2 5
7 9 6
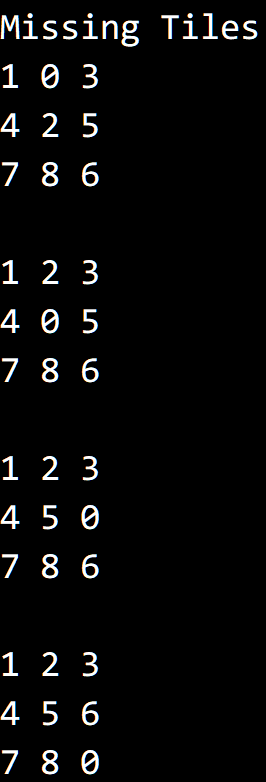

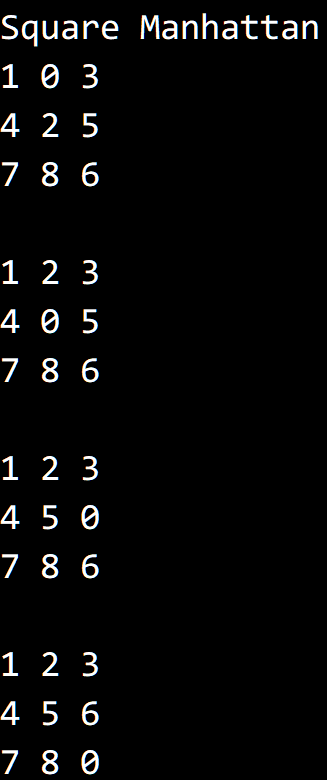
代码 #
A* 算法的泛型实现
public abstract class AStar<T> where T : IComparable<T>
{
/// <summary>
/// 相等比较器。
/// </summary>
private readonly IEqualityComparer<T> _equalityComparer;
/// <summary>
/// 默认相等比较器。
/// </summary>
private class DefaultEqualityComparer : IEqualityComparer<T>
{
public bool Equals(T x, T y)
{
Debug.Assert(x != null, nameof(x) + " != null");
return x.Equals(y);
}
public int GetHashCode(T obj)
{
return obj.GetHashCode();
}
}
/// <summary>
/// 根据 FScore 进行比较的比较器。
/// </summary>
private class FScoreComparer : IComparer<T>
{
private readonly Dictionary<T, int> _fScore;
public FScoreComparer(Dictionary<T, int> fScore)
{
_fScore = fScore;
}
public int Compare(T x, T y)
{
if (!_fScore.ContainsKey(x!))
_fScore[x] = int.MaxValue;
if (!_fScore.ContainsKey(y!))
_fScore[y] = int.MaxValue;
return _fScore[x].CompareTo(_fScore[y]);
}
}
/// <summary>
/// 新建一个 Astar 寻路器,使用元素默认相等比较器。
/// </summary>
protected AStar() : this(new DefaultEqualityComparer()) { }
/// <summary>
/// 新建一个 AStar 寻路器。
/// </summary>
/// <param name="equalityComparer">用于确定状态之间相等的比较器。</param>
protected AStar(IEqualityComparer<T> equalityComparer)
{
_equalityComparer = equalityComparer;
}
/// <summary>
/// 获得最短路径。
/// </summary>
/// <param name="start">起始状态。</param>
/// <param name="goal">终止状态。</param>
/// <returns><paramref name="start"/> 至 <paramref name="goal"/> 之间的最短路径。</returns>
public T[] GetPath(T start, T goal)
{
var comeFrom = new Dictionary<T, T>(_equalityComparer);
var gScore = new Dictionary<T, int>(_equalityComparer);
var fScore = new Dictionary<T, int>(_equalityComparer);
var openSet = new MinPq<T>(new FScoreComparer(fScore), _equalityComparer);
var closeSet = new HashSet<T>(_equalityComparer);
openSet.Insert(start);
gScore.Add(start, 0);
fScore.Add(start, HeuristicDistance(start, goal));
while (!openSet.IsEmpty())
{
var current = openSet.DelMin();
if (_equalityComparer.Equals(current, goal))
return ReconstructPath(comeFrom, current);
closeSet.Add(current);
var neighbors = GetNeighbors(current);
foreach (var neighbor in neighbors)
{
if (closeSet.Contains(neighbor))
continue;
var gScoreTentative = gScore[current] + ActualDistance(current, neighbor);
// 新状态
if (!openSet.Contains(neighbor))
openSet.Insert(neighbor);
else if (gScoreTentative >= gScore[neighbor])
continue;
// 记录新状态
comeFrom[neighbor] = current;
gScore[neighbor] = gScoreTentative;
fScore[neighbor] = gScore[neighbor] + HeuristicDistance(neighbor, goal);
}
}
return null;
}
/// <summary>
/// 倒回重建最佳路径。
/// </summary>
/// <param name="comeFrom">包含所有状态的数组。</param>
/// <param name="current">当前状态位置。</param>
/// <returns>重建之后的最短路径。</returns>
private T[] ReconstructPath(Dictionary<T, T> comeFrom, T current)
{
var pathReverse = new Stack<T>();
while (comeFrom.ContainsKey(current))
{
pathReverse.Push(current);
current = comeFrom[current];
}
var path = new T[pathReverse.Count];
for (var i = 0; i < path.Length; i++)
{
path[i] = pathReverse.Pop();
}
return path;
}
/// <summary>
/// 计算两个状态之间的估计距离,即 h(n)。
/// </summary>
/// <param name="start">初始状态。</param>
/// <param name="goal">目标状态。</param>
/// <returns>估计距离。</returns>
protected abstract int HeuristicDistance(T start, T goal);
/// <summary>
/// 计算两个状态之间的实际距离,即 g(n)。
/// </summary>
/// <param name="start">初始状态。</param>
/// <param name="goal">目标状态。</param>
/// <returns>实际距离。</returns>
protected abstract int ActualDistance(T start, T goal);
/// <summary>
/// 获得当前状态的周围状态。
/// </summary>
/// <param name="current">当前状态。</param>
/// <returns>保存周围状态的数组。</returns>
protected abstract T[] GetNeighbors(T current);
}