2.5.19

2.5.19 #

解答 #

官方解答： Kendall Tau：https://algs4.cs.princeton.edu/25applications/KendallTau.java.html

Inversion：https://algs4.cs.princeton.edu/22mergesort/Inversions.java.html

由书中 2.5.3.2 节得，两个数组之间的 Kendall Tau 距离即为两数组之间顺序不同的数对数目。

如果能够把其中一个数组变成标准排列（即 1,2,3,4... 这样的数组），

那么此时 Kendall Tau 距离就等于另一个数组中的逆序对数量。

现在我们来解决如何把一个数组 a 变成标准排列的方法。

也就是找到函数 $ f(x) $，使得 $ f(a[i])=i $ ，这样的函数其实就是数组 a 的逆数组。

如下图所示，逆数组 ainv 即为满足 ainv[a[i]] = i 的数组。

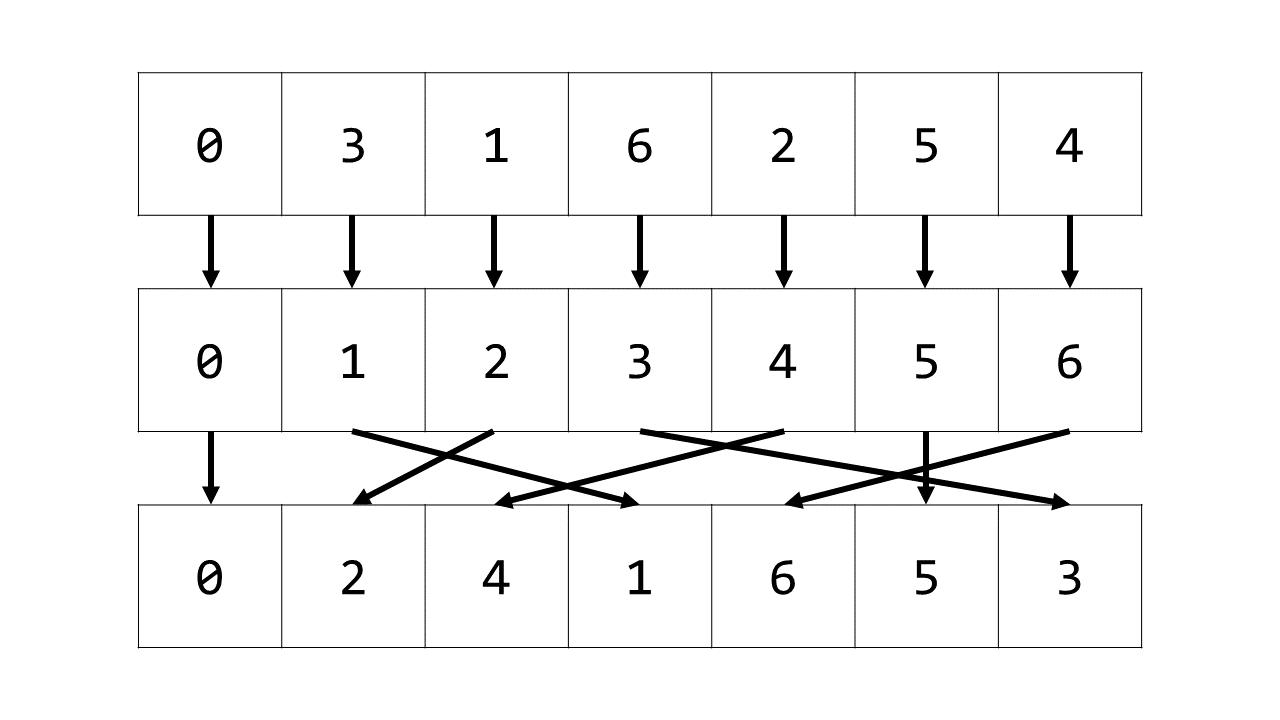
获得逆数组之后，对另一个数组 b 做同样的变换，令数组 bnew[i] = ainv[b[i]] 。

即 ainv[a[i]] = i, ainv[b[i]] = bnew[i] 。

于是问题转化为了 bnew 和标准排列之间的 Kendall Tau 距离，即 bnew 的逆序对数量。

逆序对数量的求法见 2-2-19。

代码 #


int[] testA = { 0, 3, 1, 6, 2, 5, 4 };
int[] testB = { 1, 0, 3, 6, 4, 2, 5 };
Console.WriteLine(Distance(testA, testB));

static long Distance(int[] a, int[] b)
{
    if (a.Length != b.Length)
        throw new ArgumentException("Array dimensions disagree");
    var n = a.Length;

    var ainv = new int[n];
    for (var i = 0; i < n; i++)
    {
        ainv[a[i]] = i;
    }

    var bnew = new int[n];
    for (var i = 0; i < n; i++)
    {
        bnew[i] = ainv[b[i]];
    }

    var inversions = new Inversions();
    inversions.Count(bnew);
    return inversions.Counter;
}