2.4.41 #
解答 #
多叉堆和二叉堆的实现上并没有很大的区别,
只不过下沉(Sink)时需要比较的子结点数量变多了,上浮时父结点的下标不再是 $\lfloor k /2 \rfloor$。
于是只要能推出 $d$ 叉堆的下标换算公式即可解决整个问题。
先考虑 $d$ 叉堆的在数组中的保存方式,
第一层显然只有根结点,第二层显然有 $d$ 个结点,第三层则有 $d \times d=d^2$ 个结点,如下图所示:

不难推出第 $k$ 层有 $d^{k-1}$ 个结点。
接下来我们对其标号,根结点为 1,以此类推,如下图:

现在我们来推导某个结点的子结点的下标公式。
结点 $i$ 的第一个子结点在哪里呢?
首先要加上本层剩下的结点,再加上它前面结点的所有子结点,再下一个就是它的第一个子结点了。
以 2 号结点为例,它是第二层的第一个结点,第二层共有 $d^{2-1}=d$ 个结点,剩下 $d-1$ 个结点。
2 号结点前面没有更多兄弟结点,于是第一个子结点下标即为 $2 + d - 1 + 1= 2 + d$。
3 号结点之后剩余 $d-2$ 个结点,加上前面 2 号结点的 $d$ 个子结点,
它的第一个子结点下标为 $3+d-2+d+1= 2+2d$。
不难发现规律,结点序号加一,子结点的下标就要对应加上 $d$(要加上前一个结点的子结点),
这个规律也可以从图上($d=3$)看出来:
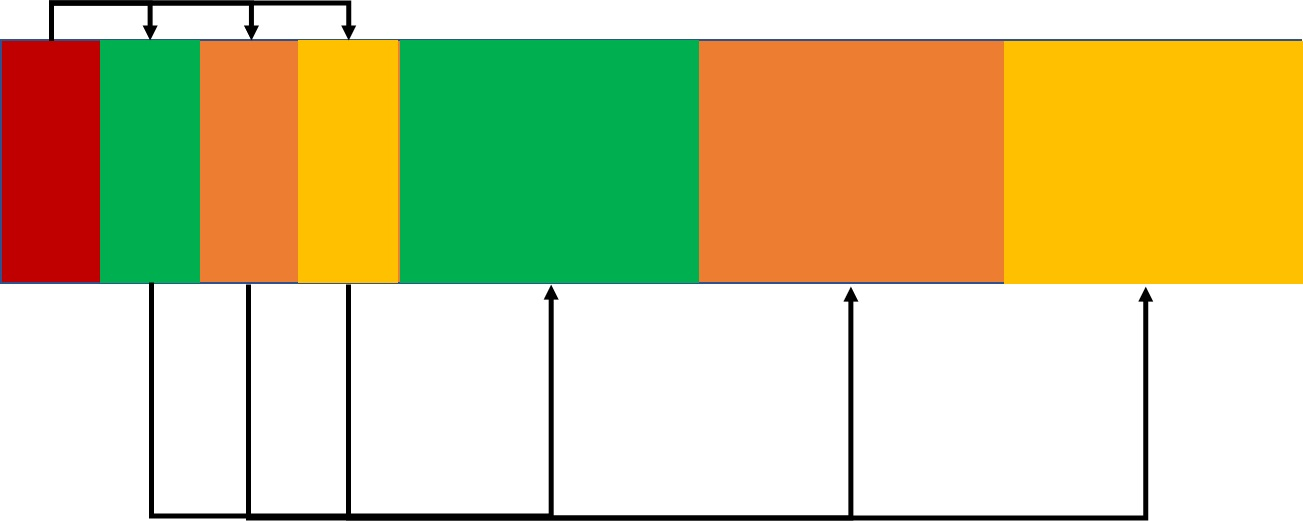
1号结点的子结点范围是 $[2,d+1]$,每加一个结点子结点就要加上 $d$ 。
于是立即可以推得结点 $i$ 的子结点下标范围是 $[d(i-1)+2,di+1]$ 。
代入 $d=2$,可以发现是符合我们已知的规律的。
接下来是结点 $i$ 的父结点,
我们由上面的式子反推可以得到父结点的下标为 $ \lfloor (i-2)/d \rfloor +1$(或者 $\lceil (i-2)/d \rceil$)。
获得这两个公式之后,只需要将 sink 和 swim 方法中上升和下降的公式做相应更改即可。
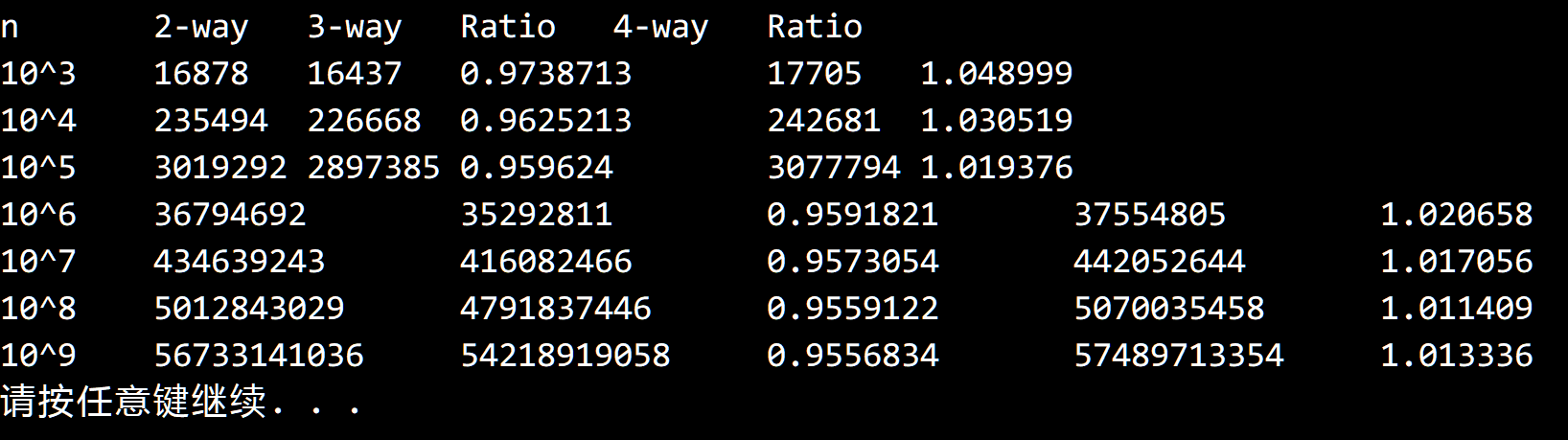
测试结果,注意下标可能会超过 int 的范围,请使用 long。:
代码 #
public static class HeapMultiway
{
/// <summary>
/// 利用堆排序对数组进行排序。
/// </summary>
/// <param name="pq">需要排序的数组。</param>
/// <param name="d">堆的分叉数。</param>
public static void Sort<T>(T[] pq, int d) where T : IComparable<T>
{
var n = pq.Length;
// 建堆
for (var k = (n - 2) / d + 1; k >= 1; k--)
{
Sink(pq, k, n, d);
}
// 排序
while (n > 1)
{
Exch(pq, 1, n--);
Sink(pq, 1, n, d);
}
}
/// <summary>
/// 令堆中的元素下沉。
/// </summary>
/// <param name="pq">需要执行操作的堆。</param>
/// <param name="k">需要执行下沉的结点下标。</param>
/// <param name="n">堆中元素的数目。</param>
/// <param name="d">堆的分叉数。</param>
private static void Sink<T>(T[] pq, int k, int n, int d) where T : IComparable<T>
{
while ((k - 1) * d + 2 <= n)
{
var j = d * (k - 1) + 2;
// 在 d 个子结点中找到最大的那个
for (int i = 0, q = j; i < d; i++)
{
if (q + i <= n && Less(pq, j, q + i))
j = q + i;
}
if (!Less(pq, k, j))
break;
Exch(pq, k, j);
k = j;
}
}
/// <summary>
/// 比较堆中下标为 <paramref name="a"/> 的元素是否小于下标为 <paramref name="b"/> 的元素。
/// </summary>
/// <param name="pq">元素所在的数组。</param>
/// <param name="a">需要比较是否较小的结点序号。</param>
/// <param name="b">需要比较是否较大的结点序号。</param>
/// <returns>如果下标为 <paramref name="a"/> 的元素较小则返回 <c>true</c>,否则返回 <c>false</c>。</returns>
private static bool Less<T>(T[] pq, int a, int b) where T : IComparable<T> => pq[a - 1].CompareTo(pq[b - 1]) < 0;
/// <summary>
/// 交换堆中的两个元素。
/// </summary>
/// <param name="pq">要交换的元素所在堆。</param>
/// <param name="a">要交换的结点序号。</param>
/// <param name="b">要交换的结点序号。</param>
private static void Exch<T>(T[] pq, int a, int b)
{
var temp = pq[a - 1];
pq[a - 1] = pq[b - 1];
pq[b - 1] = temp;
}
}