2.4.35 #
解答 #
本题有两个翻译错误。
random() ——返回索引 i 的概率是 p[i]/T,而非返回概率和索引。(return an index i with probability p[i]/T)
最后一句指的是像堆那样使用数组而非显式指针实现二叉树。(Avoid explicit pointers, as we do for heaps.)
提示已经给出了实现方案,我们用一个例子来简单说明一下。
现在给出一个分布 p,总和 T=1,如下图所示:
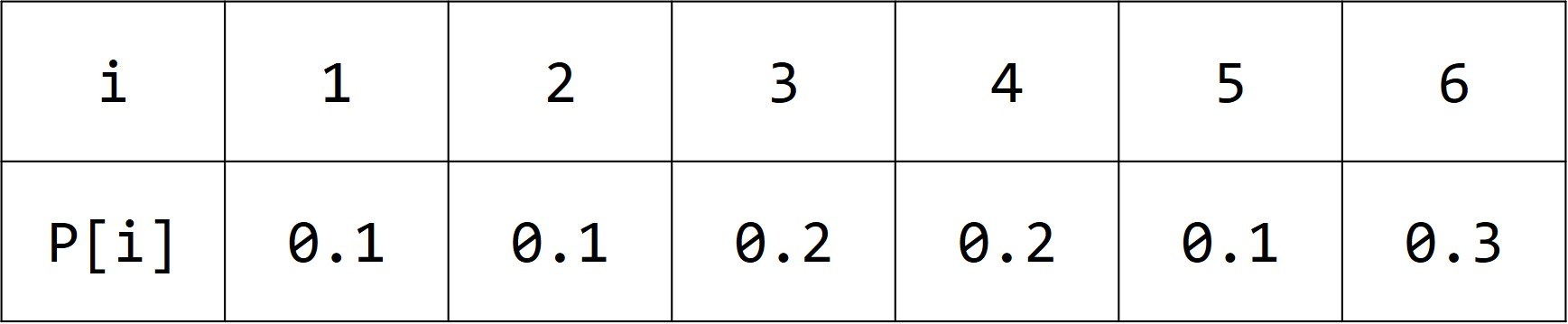
为了实现这样的随机分布,我们在 0~T 之间随机一个小数,然后根据结果返回不同的值。

现在我们将这个思想应用到完全二叉树上。
每次随机的过程其实构成了一棵选择树,我们把数组 p 当作一棵树,如下图:

为方便起见,我们重新排列一下之前的随机表:

每个值的概率并没有改变,只是每个值对应的区段换了一下。
经过这样的变换后,你会发现,如果从根结点的角度看:
如果随机的值小于 0.1,对应的编号就是 1。
如果随机的值大于 0.5,那么对应编号只能是 3 或 6,即根结点的右子树。
其他情况对应编号在左子树上。
扩展到一般情况,就变成了:
如果随机数小于当前结点,直接返回当前结点的编号。
如果随机数大于左子树权值总和+当前结点的权值,减去它们,移动到右子树。
其他情况减去当前结点的权值并移动到左子树。
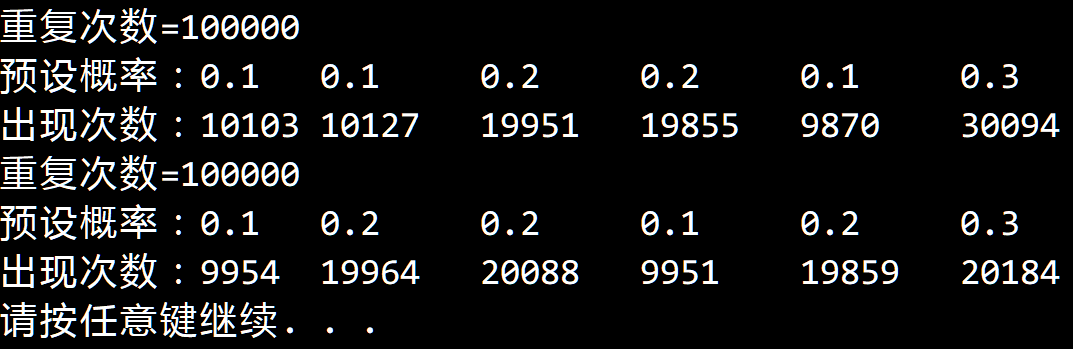
思想理解之后,代码实现就比较容易了,做了 100000 次实验的结果如下:
代码 #
internal class Sample
{
public double[] P;
public double[] SumP;
public double T;
private readonly Random _random = new();
/// <summary>
/// 构造一个离散取样类。
/// </summary>
/// <param name="data">取样数据。</param>
public Sample(double[] data)
{
// 复制权重
P = new double[data.Length + 1];
for (var i = 1; i <= data.Length; i++)
{
P[i] = data[i - 1];
T += data[i - 1];
}
// 记录子树权重之和
SumP = new double[data.Length + 1];
for (var i = data.Length; i / 2 > 0; i--)
{
SumP[i / 2] += SumP[i] + P[i];
}
}
/// <summary>
/// 根据构造时给定的取样概率返回索引。
/// </summary>
/// <returns></returns>
public int Random()
{
var weight = _random.NextDouble() * T;
var index = 1;
while (index * 2 <= P.Length)
{
// 找到结点
if (weight <= P[index]) break;
// 减去当前结点,向子结点搜寻
weight -= P[index];
index *= 2;
// 在左子树范围内
if (weight <= SumP[index] + P[index]) continue;
// 在右子树范围内,减去左子树
weight -= SumP[index] + P[index];
index++;
}
return index - 1;
}
/// <summary>
/// 修改索引 <paramref name="i"/> 的权重为 <paramref name="v"/>。
/// </summary>
/// <param name="i">需要修改的索引。</param>
/// <param name="v">新的权重。</param>
public void Change(int i, double v)
{
i += 1;
T = T - P[i] + v;
P[i] = v;
// 重新计算总和
while (i > 1)
{
i /= 2;
SumP[i] = P[i * 2] + SumP[i * 2];
if (i * 2 + 1 < P.Length)
{
SumP[i] += P[i * 2 + 1] + SumP[i * 2 + 1];
}
}
}
}