2.4.30 #
解答 #
单独用一个变量存放中位数,然后前半部分元素放在一个最大堆中,后半部分元素放在一个最小堆中。
如下图所示,注意 Median 和两个堆并没有直接连接,这里只是方便理解元素顺序。
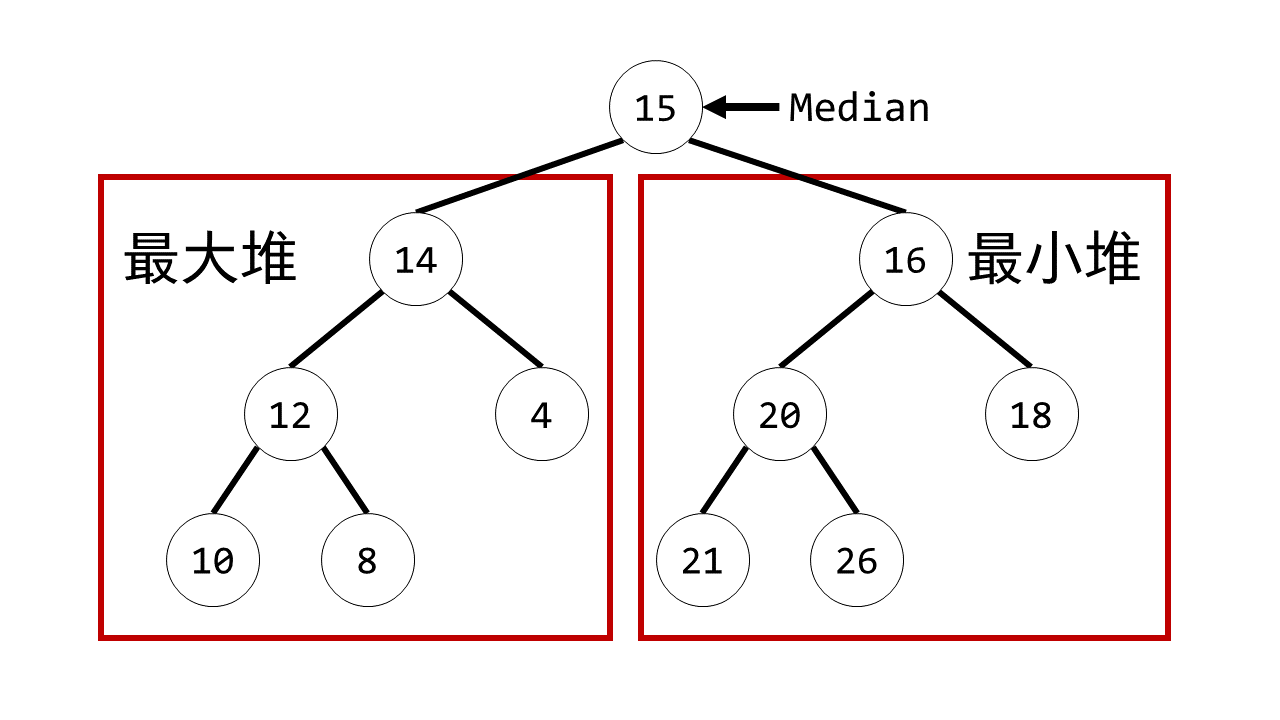
只要左右两个堆含有元素之差不超过 1,那么 Median 变量中存放的就是整个数组的中位数。
如果元素差大于 1,就需要进行调整,
把 Median 变量中存放的值插入到元素较少的堆,
再从元素较多的堆中取出元素放入 Median 变量,直到元素差不大于 1。
插入元素时,根据插入元素的大小插入到某一个堆中去,再做一次调整。
删除中位数时,去掉中位数,然后从元素较多的一侧堆中取元素补位,再进行一次调整。
编写代码时要注意堆中只有一个元素的情况需要特殊处理。
代码 #
面向中位数的堆(MedianPQ.cs)
public class MedianPq<TKey> where TKey : IComparable<TKey>
{
/// <summary>
/// 最大堆(保存前半段元素)。
/// </summary>
/// <value>最大堆(保存前半段元素)。</value>
private readonly MaxPq<TKey> _maxPq;
/// <summary>
/// 最小堆(保存后半段元素)。
/// </summary>
/// <value>最小堆(保存后半段元素)。</value>
private readonly MinPq<TKey> _minPq;
/// <summary>
/// 中位数。
/// </summary>
/// <value>中位数。</value>
private TKey _median;
/// <summary>
/// 堆的大小。
/// </summary>
/// <value>堆的大小。</value>
private int _n;
/// <summary>
/// 默认构造函数,构造一个面向中位数的堆。
/// </summary>
public MedianPq()
{
_maxPq = new MaxPq<TKey>();
_minPq = new MinPq<TKey>();
_median = default;
_n = 0;
}
/// <summary>
/// 构造一个指定容量的面向中位数的堆。
/// </summary>
/// <param name="capacity">初始容量。</param>
public MedianPq(int capacity)
{
_maxPq = new MaxPq<TKey>((capacity - 1) / 2);
_minPq = new MinPq<TKey>((capacity - 1) / 2);
_n = 0;
_median = default;
}
/// <summary>
/// 根据指定数组初始化面向中位数的堆。
/// </summary>
/// <param name="keys">初始数组。</param>
public MedianPq(TKey[] keys)
{
_minPq = new MinPq<TKey>();
_maxPq = new MaxPq<TKey>();
if (keys.Length == 0)
{
_n = 0;
_median = default;
return;
}
_n = keys.Length;
_median = keys[0];
for (var i = 1; i < keys.Length; i++)
{
if (_median.CompareTo(keys[i]) < 0)
_minPq.Insert(keys[i]);
else
_maxPq.Insert(keys[i]);
}
UpdateMedian();
}
/// <summary>
/// 向面向中位数的堆中插入一个元素。
/// </summary>
/// <param name="key">需要插入的元素。</param>
public void Insert(TKey key)
{
if (_n == 0)
{
_n++;
_median = key;
return;
}
if (key.CompareTo(_median) < 0)
_maxPq.Insert(key);
else
_minPq.Insert(key);
_n++;
UpdateMedian();
}
/// <summary>
/// 删除并返回中位数。
/// </summary>
/// <returns>中位数。</returns>
/// <exception cref="ArgumentOutOfRangeException">当堆为空时抛出该异常。</exception>
/// <remarks>如果希望获得中位数但不将其删除,请使用 <see cref="Median"/>。</remarks>
public TKey DelMedian()
{
if (IsEmpty())
throw new InvalidOperationException("MedianPQ underflow!");
var median = _median;
if (_n == 1)
{
_n--;
_median = default;
return median;
}
// 从较大的一侧堆中取元素作为新的中位数。
if (_minPq.Size() > _maxPq.Size())
_median = _minPq.DelMin();
else
_median = _maxPq.DelMax();
_n--;
return median;
}
/// <summary>
/// 获得中位数。
/// </summary>
/// <returns>中位数。</returns>
/// <remarks>如果希望删除并返回中位数,请使用 <see cref="DelMedian"/>。</remarks>
public TKey Median() => _median;
/// <summary>
/// 判断堆是否为空。
/// </summary>
/// <returns>若堆为空则返回 <c>true</c>,否则返回 <c>false</c>。</returns>
public bool IsEmpty() => _n == 0;
/// <summary>
/// 更新中位数的值。
/// </summary>
private void UpdateMedian()
{
// 根据两个堆的大小调整中位数
while (_maxPq.Size() - _minPq.Size() > 1)
{
_minPq.Insert(_median);
_median = _maxPq.DelMax();
}
while (_minPq.Size() - _maxPq.Size() > 1)
{
_maxPq.Insert(_median);
_median = _minPq.DelMin();
}
}
}