2.4.28 #
解答 #
开始时让 N=10^5,在 M=10^4 不变的情况下令 N 不断翻倍,求出算法增长的数量级。
再根据求出的增长的数量级估计 N=10^8 时所需要的时间。
为了方便比较,需要编写一个欧几里得距离类,
构造时输入一个点的坐标,内部自动计算并保存这个点到原点的欧几里得距离。
欧几里得距离的计算公式如下:
$$ d(x,y)=\sqrt{\sum_{i=1}^{n}(x_i-y_i)^2} $$
其中,x 和 y 分别代表两个点。
在本题中,y 始终是原点,且使用三维坐标系,因此公式可以简化为:
$$ d=\sqrt {x^2+y^2+z^2} $$
同时这个类需要实现 IComparable 接口以作为最小堆的元素。
做测试时,先随机生成 N 个点,再建立一个最小堆。
随后开始计时,把开始的 m 个点插入。
剩余的 n-m 个点则是先删除最小值再插入,这样可以保证最小堆的大小不变。
最后再把堆中的所有元素输出,停止计时。
用不断倍增的的 N 值做上述测试,获得每次的耗时,进而求得算法增长的数量级。
求得的结果如下:
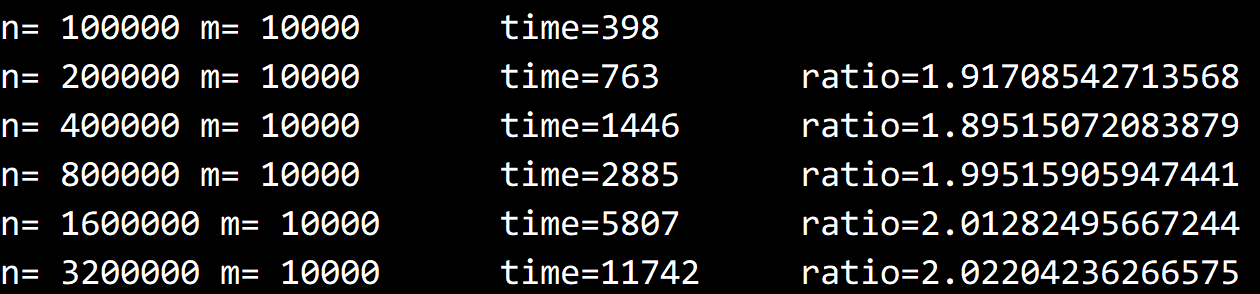
可以推出当 N=10^8 时耗时为 $ 398 \ ms × 1000 = 398 \ s $
代码 #
欧几里得距离类,EuclideanDistance3D
internal class EuclideanDistance3D : IComparable<EuclideanDistance3D>
{
private readonly int _x, _y, _z;
private readonly double _distance;
/// <summary>
/// 计算点到原点的欧几里得距离。
/// </summary>
/// <param name="x">x 轴坐标。</param>
/// <param name="y">y 轴坐标。</param>
/// <param name="z">z 轴坐标。</param>
public EuclideanDistance3D(int x, int y, int z)
{
_x = x;
_y = y;
_z = z;
_distance = Math.Sqrt(x * x + y * y + z * z);
}
/// <summary>
/// 比较两个欧几里得距离的大小。
/// </summary>
/// <param name="other">另一个欧几里得距离。</param>
/// <returns></returns>
public int CompareTo(EuclideanDistance3D other)
{
return _distance.CompareTo(other._distance);
}
/// <summary>
/// 以 "(x, y, z)" 形式输出点的坐标。
/// </summary>
/// <returns></returns>
public override string ToString()
{
return "(" + _x + ", " + _y + ", " + _z + ")";
}
}