2.4.24 #
解答 #
链式实现,每个结点都包含一个指向父结点的指针和两个指向子结点的指针。
交换结点可以直接用交换两个结点的值来实现(与数组的实现一样),而不是对两个结点的指针进行交换。
于是 Sink() 和 Swim() 操作就比较简单,直接按照定义实现即可。
比较困难的是删除和插入结点,或者更具体的说,
如何找到按照完全二叉树定义下序号向后/向前一位的结点?
我们首先在堆里面维护两个指针,一个指向根结点(root),另一个指向当前最后一个结点(last)。
当需要插入新结点时,我们需要找到 last 的后一位的父结点,然后把新的结点插入为该结点的左子结点。
这段话可能比较绕,下面这个示意图可以帮助理解,有三种情况:
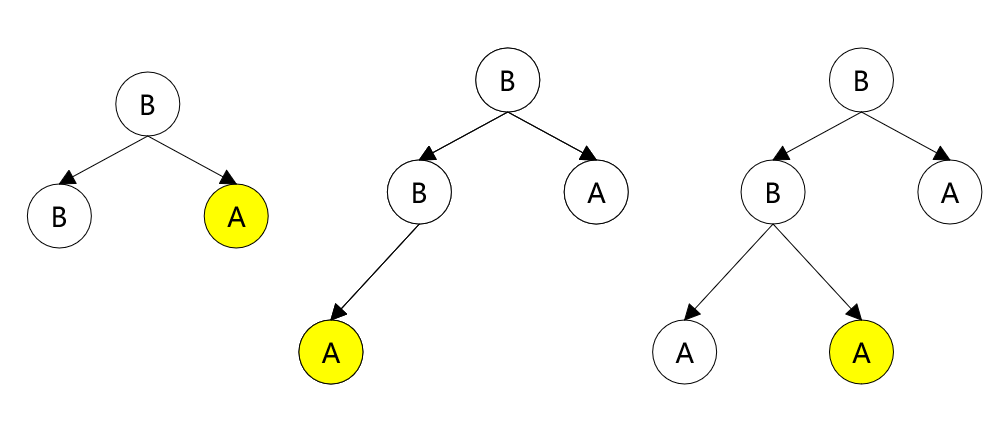
标黄的代表 last 指着的位置。
我们先从简单的说起,中间的第二种情况,新插入的结点应该放在右侧,即作为 last 的父结点的右子结点。
如果 last 已经是右子结点了,那么就考虑第三种情况。
此时应该向上回溯,直到在某一次回溯中,结点是从父结点的左侧回溯上来的 (即图中路径 A-B-B,B-B 这一步是从左子树回溯上来的)。
于是待插入的位置就在该父结点的右子树的最左侧结点(即图中根结点的右子结点 A)。
最后是图中第一种情况,整棵树已经是满二叉树了。
这种情况下会一路回溯到根结点,那么只要一路下沉到最左侧的叶子结点,把新结点插入到其左子树上即可。
删除结点同理,也是这三种情况,只是需要找前一个结点,判断条件中的左右正好相反。
如果已经是右子结点了,只需要把 last 改为其父结点的左子树即可。
如果是左子结点,就需要回溯,直到某一次回溯是从右子树回溯上来的,last 应该指向其左子树的最右侧结点。
如果删除后正好变成满二叉树,那么会一直回溯到根结点,last 应该指向整棵树的最右侧结点。
代码实现中还需要处理只有一个结点以及没有结点时的特殊情况。
根据上面的算法,插入/删除找到相应位置所需的最大耗时为 2lgN (从树的一侧回溯到根结点,再下沉到另一侧的底部)。
Sink 和 Swim 是 O(lgN) 级的,因此整个插入/删除操作是 O(lgN) 的。
代码 #
public class MaxPqLinked<TKey> : IMaxPq<TKey> where TKey : IComparable<TKey>
{
/// <summary>
/// 二叉堆的根结点。
/// </summary>
private TreeNode<TKey> _root;
/// <summary>
/// 二叉堆的最后一个结点。
/// </summary>
private TreeNode<TKey> _last;
/// <summary>
/// 二叉堆中的结点个数。
/// </summary>
private int _nodesCount;
/// <summary>
/// 删除并返回最大值。
/// </summary>
/// <returns>最大值。</returns>
/// <remarks>如果希望获得最大值而不删除它,请使用 <see cref="Max"/>。</remarks>
public TKey DelMax()
{
var result = _root.Value;
Exch(_root, _last);
if (_nodesCount == 2)
{
_root.Left = null;
_last = _root;
_nodesCount--;
return result;
}
if (_nodesCount == 1)
{
_last = null;
_root = null;
_nodesCount--;
return result;
}
// 获得前一个结点。
var newLast = _last;
if (newLast == _last.Prev.Right)
newLast = _last.Prev.Left;
else
{
// 找到上一棵子树。
while (newLast != _root)
{
if (newLast != newLast.Prev.Left)
break;
newLast = newLast.Prev;
}
// 已经是满二叉树。
if (newLast == _root)
{
// 一路向右,回到上一层。
while (newLast.Right != null)
newLast = newLast.Right;
}
// 不是满二叉树。
else
{
// 向左子树移动,再一路向右。
newLast = newLast.Prev.Left;
while (newLast.Right != null)
newLast = newLast.Right;
}
}
// 删除最后一个结点。
if (_last.Prev.Left == _last)
_last.Prev.Left = null;
else
_last.Prev.Right = null;
Sink(_root);
// 指向新的最后一个结点。
_last = newLast;
_nodesCount--;
return result;
}
/// <summary>
/// 插入一个新的结点。
/// </summary>
/// <param name="v">待插入的结点。</param>
public void Insert(TKey v)
{
var item = new TreeNode<TKey>(v);
// 堆为空。
if (_last == null)
{
_root = item;
_last = item;
_nodesCount++;
return;
}
// 堆只有一个结点。
if (_last == _root)
{
item.Prev = _root;
_root.Left = item;
_last = item;
_nodesCount++;
Swim(item);
return;
}
// 定位到最后一个节点的父结点。
var prev = _last.Prev;
// 右子节点为空,插入到右子节点。
if (prev.Right == null)
{
item.Prev = prev;
prev.Right = item;
}
else
{
// 当前子树已满,需要向上回溯。
// 找到下一个子树(回溯的时候是从左子树回溯上去的)。
while (prev != _root)
{
if (prev != prev.Prev.Right)
break;
prev = prev.Prev;
}
// 已经是满二叉树。
if (prev == _root)
{
// 一路向左,进入下一层。
while (prev.Left != null)
prev = prev.Left;
item.Prev = prev;
prev.Left = item;
}
// 不是满二叉树。
else
{
// 向右子树移动,再一路向左。
prev = prev.Prev.Right;
while (prev.Left != null)
prev = prev.Left;
item.Prev = prev;
prev.Left = item;
}
}
_last = item;
_nodesCount++;
Swim(item);
}
/// <summary>
/// 返回二叉堆是否为空。
/// </summary>
/// <returns>如果为空则返回 <c>true</c>,否则返回 <c>false</c>。</returns>
public bool IsEmpty() => _root == null;
/// <summary>
/// 返回二叉堆中的最大值。
/// </summary>
/// <returns>堆中的最大值。</returns>
/// <remarks>如果希望删除并返回最大元素,请使用 <see cref="DelMax"/>。</remarks>
public TKey Max() => _root.Value;
/// <summary>
/// 返回二叉堆中的元素个数。
/// </summary>
/// <returns>堆中元素数量。</returns>
public int Size() => _nodesCount;
/// <summary>
/// 使结点上浮。
/// </summary>
/// <param name="k">需要上浮的结点。</param>
private void Swim(TreeNode<TKey> k)
{
while (k.Prev != null)
{
if (Less(k.Prev, k))
{
Exch(k.Prev, k);
k = k.Prev;
}
else
break;
}
}
/// <summary>
/// 使结点下沉。
/// </summary>
/// <param name="k">需要下沉的结点。</param>
private void Sink(TreeNode<TKey> k)
{
while (k?.Left != null || k?.Right != null)
{
TreeNode<TKey> toExch;
if (k.Left != null && k.Right != null)
toExch = Less(k.Left, k.Right) ? k.Right : k.Left;
else if (k.Left != null)
toExch = k.Left;
else
toExch = k.Right;
if (Less(k, toExch))
Exch(k, toExch);
else
break;
k = toExch;
}
}
/// <summary>
/// 交换二叉堆中的两个结点。
/// </summary>
/// <param name="a">要交换的第一个结点。</param>
/// <param name="b">要交换的第二个结点。</param>
private void Exch(TreeNode<TKey> a, TreeNode<TKey> b)
{
var temp = a.Value;
a.Value = b.Value;
b.Value = temp;
}
/// <summary>
/// 比较第一个结点值的是否小于第二个。
/// </summary>
/// <param name="a">判断是否较小的结点。</param>
/// <param name="b">判断是否较大的结点。</param>
/// <returns>如果 <paramref name="a"/> 较小则返回 <c>true</c>,否则返回 <c>false</c>。</returns>
private bool Less(TreeNode<TKey> a, TreeNode<TKey> b)
=> a.Value.CompareTo(b.Value) < 0;
}