2.4.14 #

解答 #

对于 n <= 2 的堆

第一步让最大元素和末端元素交换。

第二步下沉时由于 n <= 1，不需要交换。

故总共发生了一次交换，两个元素发生了交换。

对于 n = 3 的堆

第一步让最大元素和末端元素交换。

第二步如果末端元素大于另一侧的子结点，那么就不需要交换。

故最优情况时总共发生一次交换，两个元素被交换。

对于 n > 3 的堆。

第一步需要让最末端元素和最大元素交换。

由于堆中第二大的元素必定位于根节点之后。

故最末端元素一定小于该第二大元素。

因此在下沉操作时必定会和第二大元素进行交换。

故至少发生两次交换，总共有三个元素发生了交换。

构造的堆（n=15）

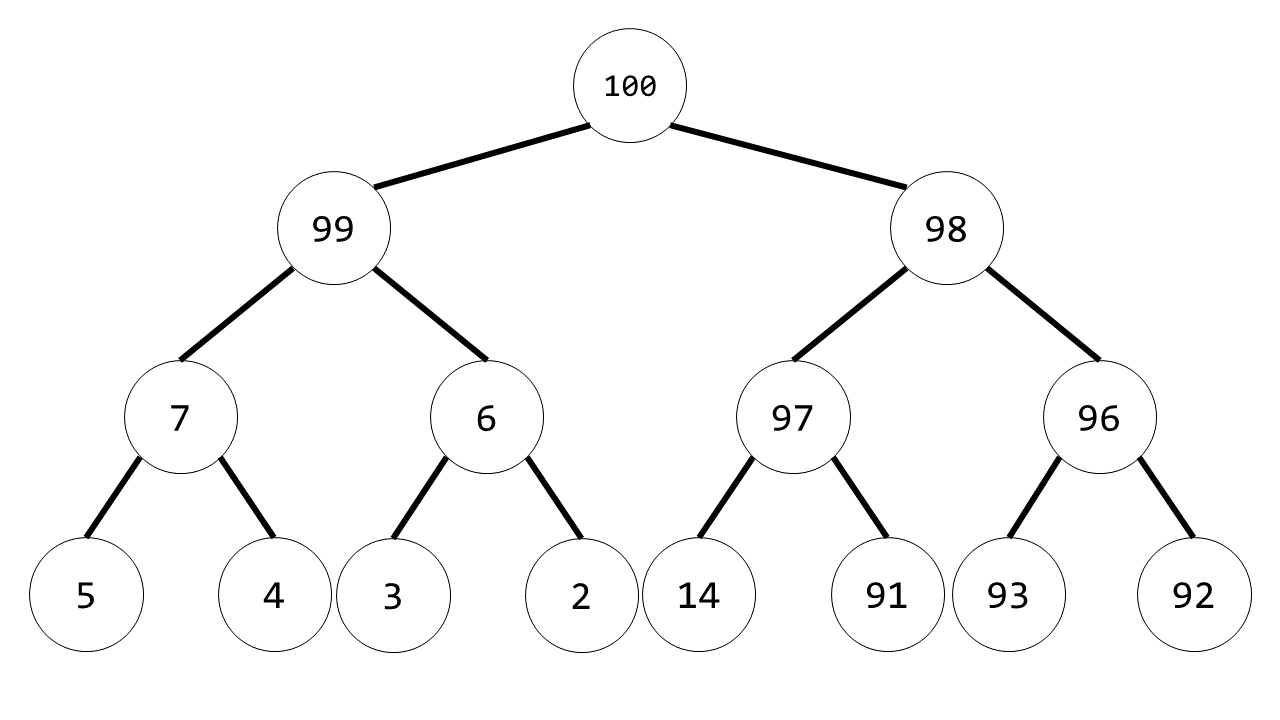
92 和 100 交换，随后 92 和 99 交换

构造最优情况堆的方式如下（取根结点为 100）：

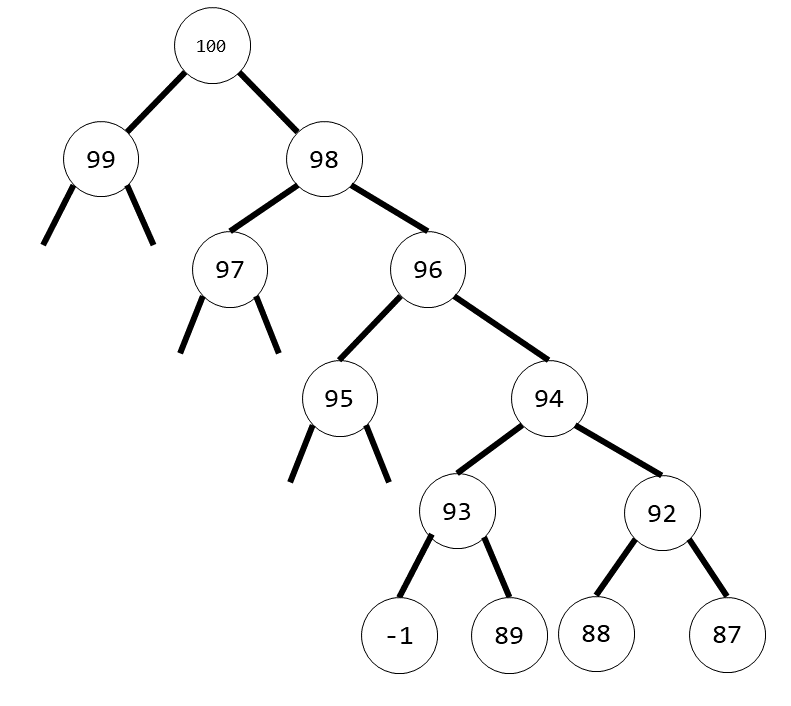
对于每个结点，左子结点大于右子结点，

且左子结点的子元素都小于右子树的最小值，

（上例中省略了这部分元素，可以将它们当作负数）

于是第一次 DelMax 的时候，只需要两次交换，三个元素被交换。（即 87 最后被交换到上例中 99 的位置）

第二次 DelMax 的时候，只需要三次交换，六个元素被交换. （88 交换到 97 的位置）

因此当 n > 7 时，连续两次 DelMax() 最少只需要 5 次交换。

第三次 DelMax 的时候，只需要四次交换，九个元素被交换。（89 交换到 95 的位置）

因此当 n > 15 时，连续三次 DelMax() 最少只需要 9 次交换。