2.3.7 #

解答 #

我讨厌数学= =

证明：

我们设 $C_0(n)$ 代表将 $n$ 个不重复元素排序时大小为 0 的数组的数量。

同理有 $C_1(n)$ 和 $C_2(n)$ 代表大小为 1 的数组的数量以及大小为 2 的数组的数量。

设 k 代表切分位置，显然切分位置随机且概率相等，在 1~n 之间均匀分布。

根据条件，$C_0(n), C_1(n),C_2(n)$ 都满足下式：

$$ C(n)= \frac{\sum_{k=1}^{n}(C(k-1)+C(n-k))}{n} $$

根据快速排序算法， $\sum_{k=1}^{n}C(k-1)=\sum_{k=1}^{n}C(n-k)$ ，因此

$$ C(n)=\frac{2\sum_{k=1}^{n}C(k-1)}{n}\newline nC(n)=2\sum_{k-1}^{n}C(k-1) $$

同理代入 $n-1$ 有

$$ (n-1)C(n-1)=2\sum_{k-1}^{n-1}C(k-1) $$

相减

$$ nC(n)-(n-1)C(n-1)=2C(n-1)\newline C(n)=\frac{n+1}{n}C(n-1) $$

利用累乘法求到通项公式

$$ \frac{C(n)}{C(n-1)}=\frac{n+1}{n} \newline \frac{C(n)}{C(n-1)}\times\frac{C(n-1)}{C(n-2)}\times\dots\times\frac{C(m+1)}{C(m)}= \frac{n+1}{n}\times\frac{n}{n-1}\times\dots\times\frac{m+2}{m+1}\newline \frac{C(n)}{C(m)}=\frac{n+1}{m+1}\newline C(n)=C(m)\frac{n+1}{m+1}，n>m $$

对于 $C_0(n)$ ，我们有初始条件 $C_0(0)=1, C_0(1)=0,C_0(2)=C_0(0)+C_0(1)=1$

$$ C_0(n)=\frac{n+1}{3}, n>2 $$

对于 $C_1(n)$ ，我们有初始条件 $C_1(0)=0,C_1(1)=1,C_1(2)=C_1(0)+C_1(1)=1$

$$ C_1(n)=\frac{n+1}{3},n>2 $$

对于 $C_2(n)$ ，我们有初始条件 $C_2(0)=C_2(1)=0,C_2(2)=1,C_2(3)=\frac{2\times(C_2(0)+C_2(1)+C_2(2))}{3}=\frac{2}{3}$

$$ C_2(n)=\frac{n+1}{6},n>3 $$

结论

$$ C_0(n)=C_1(n)=\frac{n+1}{3},n>2 \newline C_2(n)=\frac{n+1}{6},n>3 $$

实验结果：

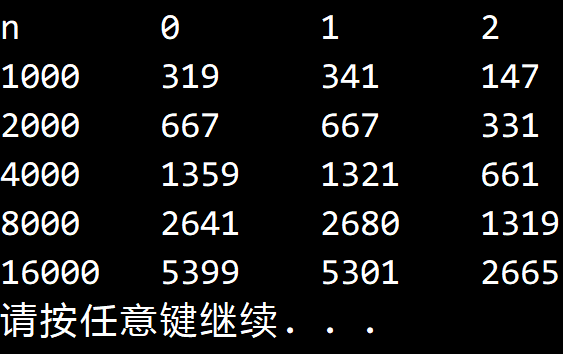
另请参阅 #

Quick 库 What is the expected number of subarrays of size 0, 1 and 2 when quicksort is used to sort an array of N items with distinct keys?-Stack Overflow