2.3.24 #
解答 #
取样排序的想法很简单:
常规快排的枢轴只有一个。
如果用一个数组来充当枢轴,根据排序位置的不同自动选择对应的枢轴,
显然能够更好的估计中位数,以求更好的切分效果。
于是引入了「取样」的概念,假如我们从源数组中随机取了 3 个元素并对其排序,
那么这 3 个元素的中位数可以作为第一次切分的枢轴,剩余两个元素则可以充当切分后两个子数组的枢轴。
那么当取样元素到达一个合适的数量时,就能达到提升切分效率的目标。
大致思路如下:
首先先从输入数组里随机取一些元素,作为「取样数组」。
用任意排序算法(比如快排)对取样数组进行排序。
(由于取样数组通常都比较小,这一步的时间消耗通常不会影响性能)
取出取样数组里面的中位数,当作枢轴对剩下的数组进行切分。
之后的切分中,根据排序区间在剩余数组中的相对位置,
用取样数组中对应位置的数作为枢轴,直到整个排序完成。
论文里提到了两种实现方式。
第一种方法
取样数组和剩余数组是分开保存的。
每次切分完成后,并不把枢轴放入剩余数组中,
而是等到剩余数组全部排序完毕之后再用一次归并(merge)操作将取样数组和剩余数组归并。
第二种方法
取样数组和剩余数组保存在同一片空间里,这也是这份题解所实现的方法。
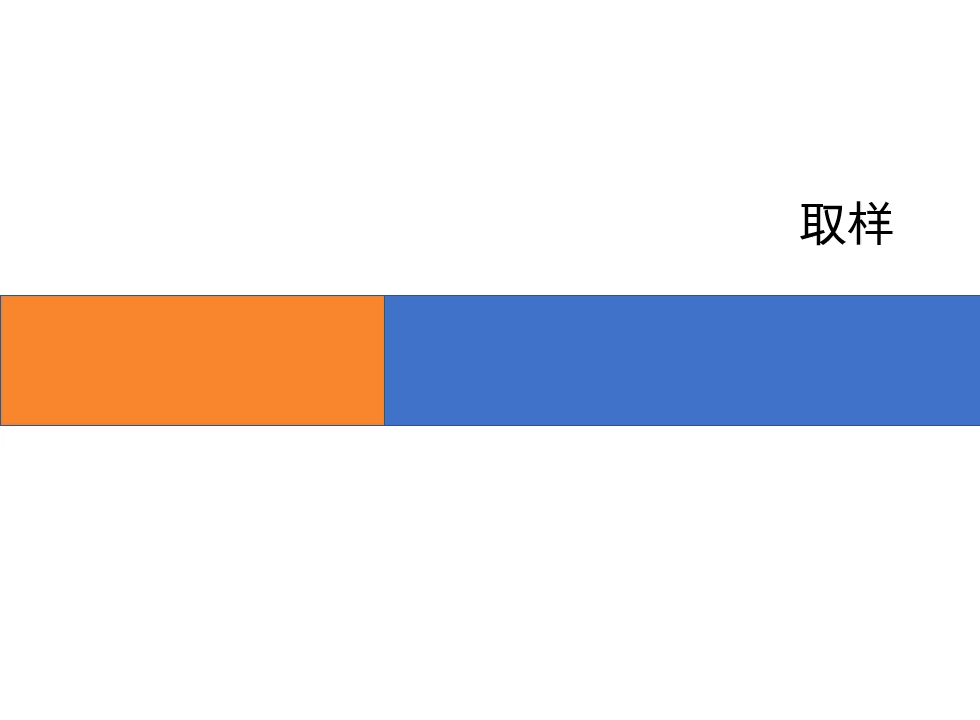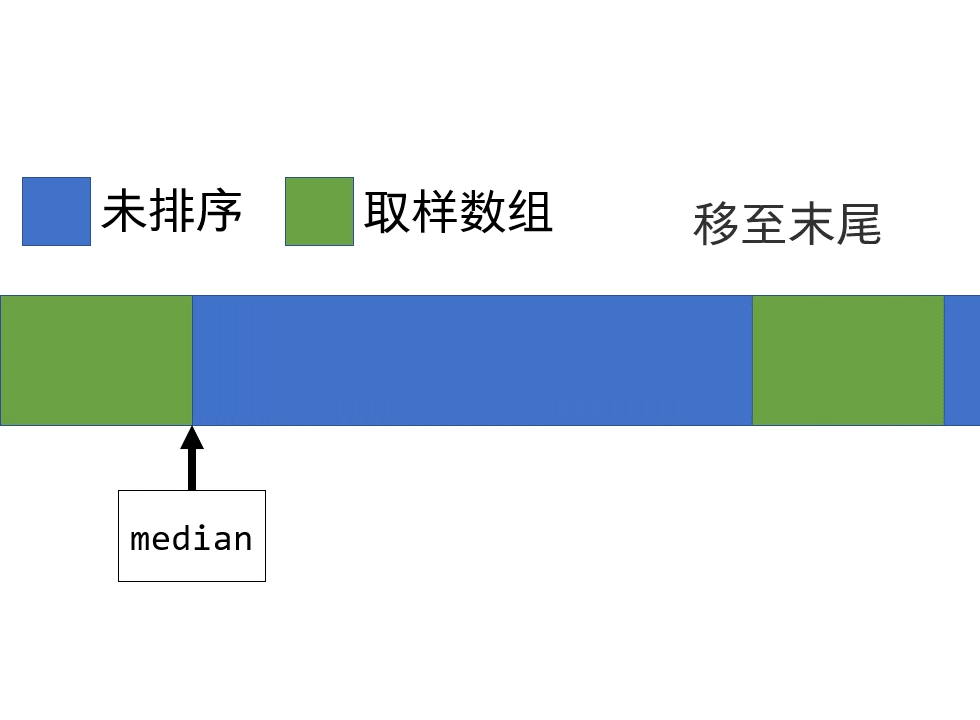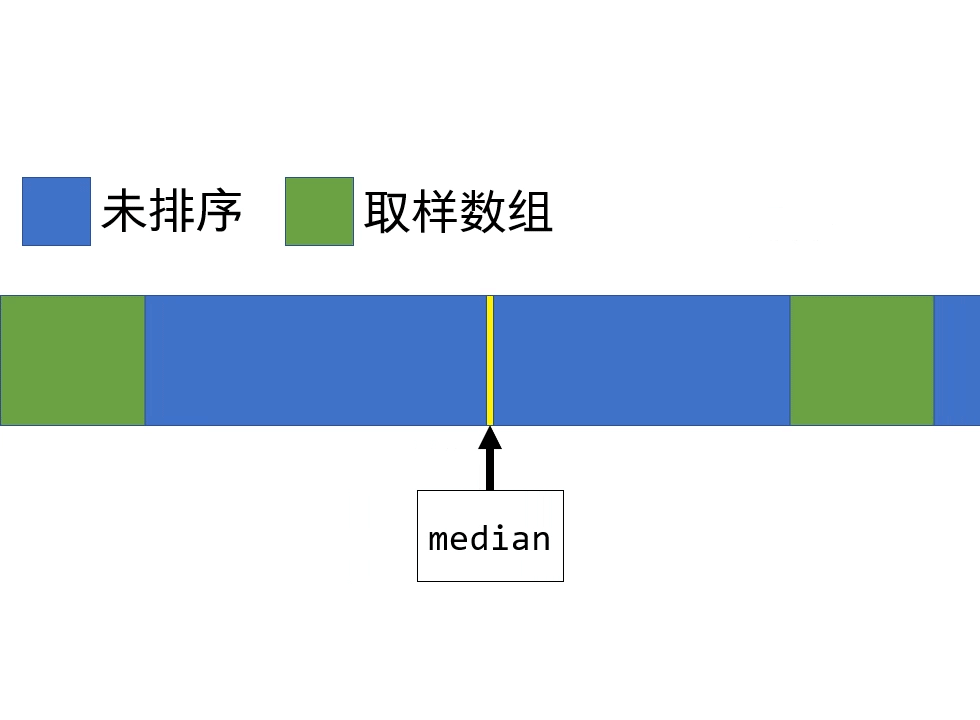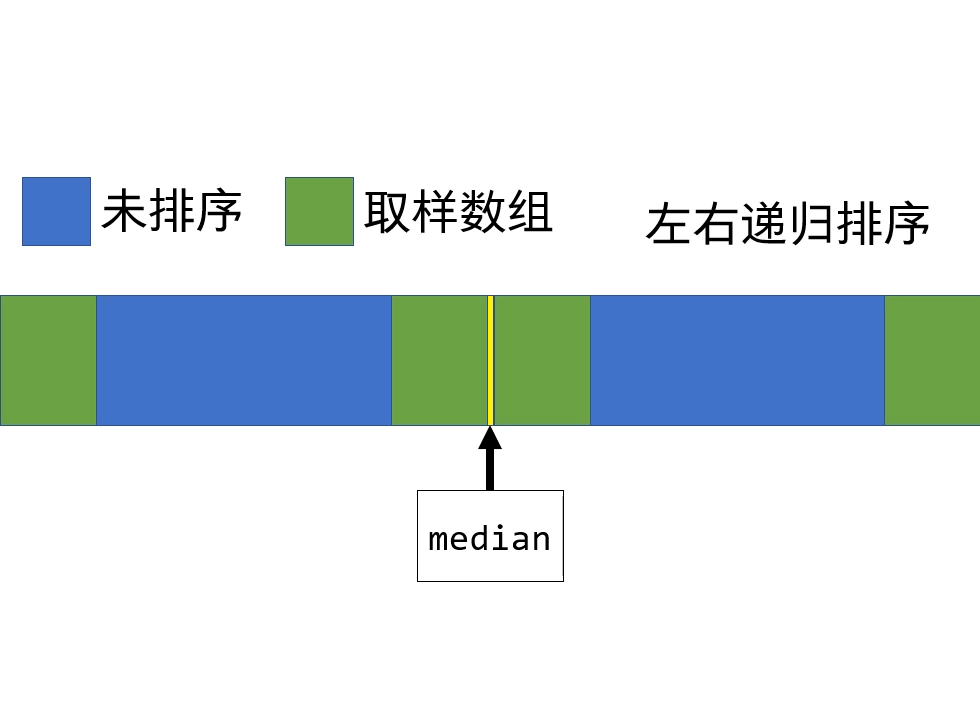
在打乱输入数组之后,取前 2^k-1 个元素作为取样数组,用快排对其排序。
然后把取样数组的后半部分放到整个数组的末尾。
这样操作的结果是输入数组分为了四个部分:
有序的取样数组、取样数组的中位数、无序的剩余数组、有序的取样数组。
中位数则位于第一部分的末尾,我们将其作为枢轴对剩余数组进行切分,数组变为:
有序的取样数组、小于中位数的部分、枢轴、大于中位数的部分、有序的取样数组
接下来我们再对第一个部分取半,放到中位数之前;对最后一部分取半,放到中位数之后:
0 ~ 1/4 取样数组、小于中位数、1/4 ~ 1/2 取样数组、枢轴、1/2~3/4 取样数组、大于中位数、3/4~1 取样数组
你会发现枢轴前后又分别变回了初始条件,递归执行上述操作,便能对整个数组排序。
注意当取样数组用完的时候,直接变回普通的快排。
现代的取样排序
这里的「现代」并不意味着更好,只是让取样排序能更好的适应多线程排序。
首先仍然是取样,取样的数量往往取决于线程的数量,比如说取了 p-1 个,就将数组分为 p 份。
对取样数组进行排序,获得 p 个区间(桶)。
遍历输入的数组,把元素扔到相应的桶里面。
把每个桶和对应的枢轴送到对应的线程进行排序。
汇总各个桶中的结果,排序完毕。
测试结果:
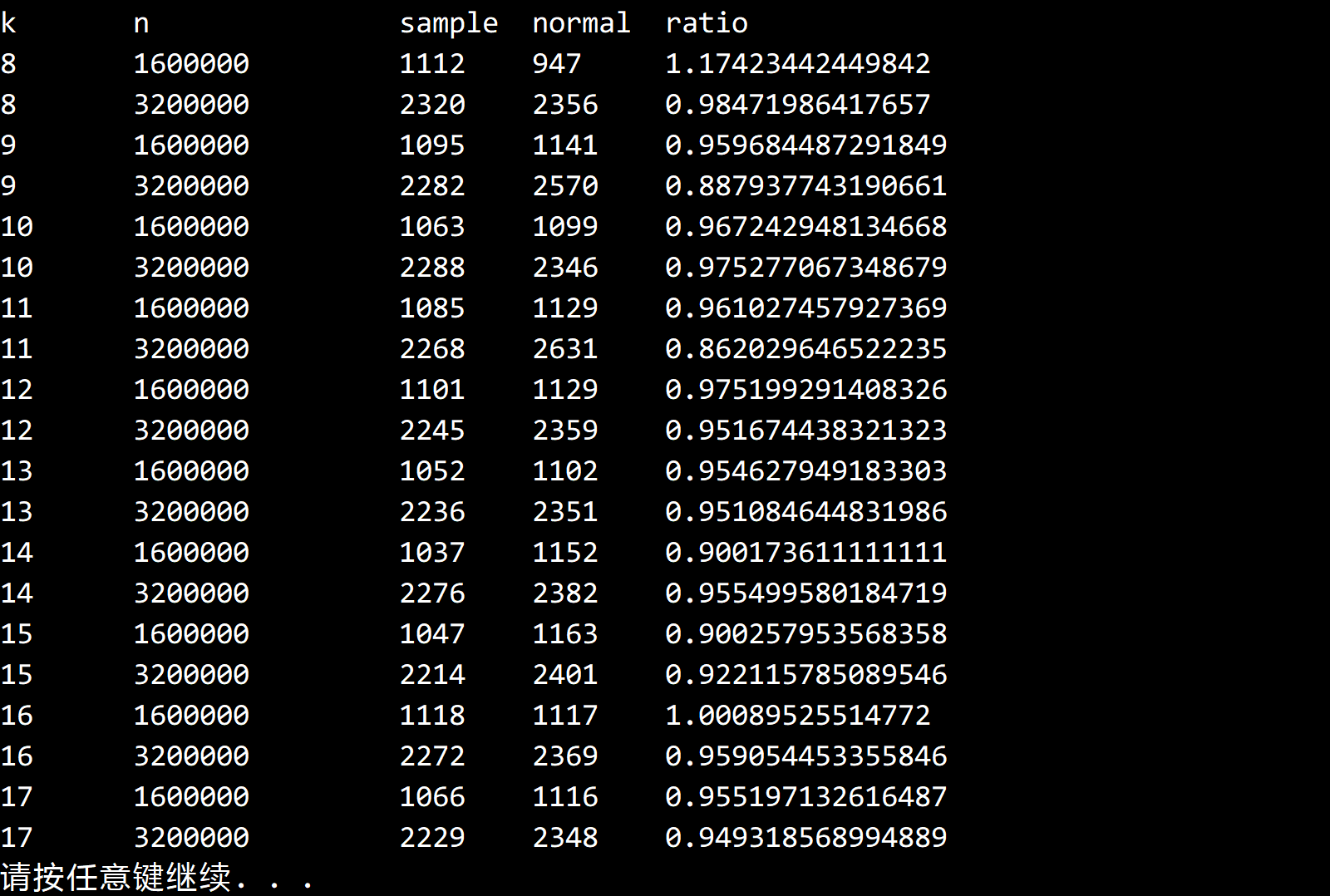
大概能提升 5%~10% 的性能。
代码 #
/// <summary>
/// 取样排序类。
/// </summary>
public class SampleSort : QuickSort
{
/// <summary>
/// 取样数组长度 2^k - 1 的阶数。
/// </summary>
/// <value>取样数组长度的阶数。</value>
public int K { get; set; }
/// <summary>
/// 默认构造函数。
/// </summary>
public SampleSort()
{
K = 8;
}
/// <summary>
/// 用快速排序对数组 a 进行升序排序。
/// </summary>
/// <typeparam name="T">需要排序的类型。</typeparam>
/// <param name="a">需要排序的数组。</param>
public override void Sort<T>(T[] a)
{
if (a.Length < Math.Pow(2, K + 1))
{
// 小于 2^(k+1) 的数组直接进行快排
base.Sort(a);
return;
}
Shuffle(a);
var samplehi = (int)Math.Pow(2, K) - 2;
// 利用快速排序对取样数组进行排序
base.Sort(a, 0, samplehi);
// 找到取样数组的中位数
var sampleMedian = samplehi / 2;
// 将取样数组后半部分放到数组末尾
int i = samplehi, j = a.Length - 1;
while (i != sampleMedian)
Exch(a, i--, j--);
// 根据取样数组进行排序
Sort(a, 0, sampleMedian, j, a.Length - 1);
Debug.Assert(IsSorted(a));
}
/// <summary>
/// 用快速排序对数组 a 的 lo ~ hi 范围排序。
/// </summary>
/// <typeparam name="T">需要排序的数组类型。</typeparam>
/// <param name="a">需要排序的数组。</param>
/// <param name="sampleLo">取样数组的起始下标。</param>
/// <param name="lo">排序范围的起始下标。</param>
/// <param name="hi">排序范围的结束下标。</param>
/// <param name="samplehi">取样数组的终止下标。</param>
private void Sort<T>(T[] a, int sampleLo, int lo, int hi, int samplehi) where T : IComparable<T>
{
if (hi <= lo) // 别越界
return;
var j = Partition(a, lo, hi);
// 将前部的有序取样数组取半,后半部分放在枢轴前面。
if (lo - sampleLo > 1)
{
// p 应该始终指向有序部分的最后一项
// v 应该始终指向有序部分的前面一项
int p = lo - 1, v = j - 1;
for (var i = 0; i < (lo - sampleLo) / 2; i++)
{
Exch(a, p--, v--);
}
Sort(a, sampleLo, p, v, j - 1);
}
else
{
// 取样数组已经用完,退化为普通 Quicksort
base.Sort(a, sampleLo, j - 1);
}
// 将尾部有序取样数组取半,前半部分放在枢轴后面。
if (samplehi - hi > 1)
{
// p 应该始终指向有序部分的前面一项
// v 应该始终指向有序部分的最后一项
int p = hi, v = j;
for (var i = 0; i < (samplehi - hi) / 2; i++)
{
Exch(a, ++p, ++v);
}
Sort(a, j + 1, v, p, samplehi);
}
else
{
// 取样数组已用完,退化为普通 Quicksort
base.Sort(a, j + 1, samplehi);
}
}
/// <summary>
/// 对数组进行切分,返回枢轴位置。
/// </summary>
/// <typeparam name="T">需要切分的数组类型。</typeparam>
/// <param name="a">需要切分的数组。</param>
/// <param name="lo">切分的起始点。</param>
/// <param name="hi">切分的末尾点。</param>
/// <returns>枢轴下标。</returns>
private int Partition<T>(T[] a, int lo, int hi) where T : IComparable<T>
{
int i = lo, j = hi + 1;
var v = a[lo];
while (true)
{
while (Less(a[++i], v))
if (i == hi)
break;
while (Less(v, a[--j]))
if (j == lo)
break;
if (i >= j)
break;
Exch(a, i, j);
}
Exch(a, lo, j);
return j;
}
/// <summary>
/// 打乱数组。
/// </summary>
/// <typeparam name="T">需要打乱的数组类型。</typeparam>
/// <param name="a">需要打乱的数组。</param>
private void Shuffle<T>(T[] a)
{
var random = new Random();
for (var i = 0; i < a.Length; i++)
{
var r = i + random.Next(a.Length - i);
var temp = a[i];
a[i] = a[r];
a[r] = temp;
}
}
}
测试用例:
var quickNormal = new QuickSort();
var sampleSort = new SampleSort();
var arraySize = 1600000; // 初始数组大小。
const int kSteps = 10; // 取样 k 值的递增次数。
const int trialTimes = 1; // 每次实验的重复次数。
const int trialLevel = 2; // 双倍递增的次数。
Console.WriteLine("k\tn\t\tsample\tnormal\tratio");
for (var i = 0; i < kSteps; i++)
{
var array = arraySize;
for (var j = 0; j < trialLevel; j++)
{
double timeSample = 0;
double timeNormal = 0;
for (var k = 0; k < trialTimes; k++)
{
var a = SortCompare.GetRandomArrayInt(array);
var b = new int[a.Length];
a.CopyTo(b, 0);
timeNormal += SortCompare.Time(quickNormal, b);
timeSample += SortCompare.Time(sampleSort, a);
}
timeSample /= trialTimes;
timeNormal /= trialTimes;
if (arraySize < 10000000)
Console.WriteLine(
sampleSort.K + "\t" + array + "\t\t" + timeSample + "\t" + timeNormal + "\t" + timeSample / timeNormal);
else
Console.WriteLine(
sampleSort.K + "\t" + array + "\t" + timeSample + "\t" + timeNormal + "\t" + timeSample / timeNormal);
array *= 2;
}
sampleSort.K++;
}
另请参阅 #
关于取样排序的论文(1970 年): Frazer W D, McKellar A C. Samplesort: A sampling approach to minimal storage tree sorting[J]. Journal of the ACM (JACM), 1970, 17(3): 496-507. 维基百科中的取样排序: Samplesort-Wikipedia 本题用到的类库链接: Quick 库