2.3.22 #
解答 #
官方实现见:https://algs4.cs.princeton.edu/23quicksort/QuickBentleyMcIlroy.java.html
快速三向切分 #
论文引用见「另请参阅」部分。
算法演示
Ninther 算法 #
官方实现中用到了 Ninther 算法用于选取近似中位数(作为枢轴),
该算法由 John Tukey 在 1978 年提出,论文引用见「另请参阅」部分。
这个算法的思想其实很简单,假设我们有三个数 $y_1, y_2, y_3$ ,那么其中位数为:
$$ y_A= {\rm median}\lbrace y_1,y_2,y_3 \rbrace $$
现在对于九个数,我们以三个为一组,取三个中位数:
$$ y_A= {\rm median}\lbrace y_1,y_2,y_3 \rbrace \newline y_B= {\rm median}\lbrace y_4,y_5,y_6 \rbrace \newline y_C= {\rm median}\lbrace y_7,y_8,y_9 \rbrace $$
接下来取这三个中位数的中位数,有:
$$ y_E= {\rm median}\lbrace y_A,y_B,y_C \rbrace $$
我们把上述过程封装成函数,即 $y_E= {\rm ninther}\lbrace y_1,y_2,\cdots,y_9 \rbrace$ 。
于是我们获得的 $y_E$ 即为近似中位数,如果 $\lbrace y_1,y_2,\cdots,y_9 \rbrace$ 是单调数列,那么 $y_E$ 就是中位数。
获取三个数中的中位数 #
事实上,我们可以直接画出三个数排列的所有可能,获得决策树。

然后根据决策树写出取中位数的算法:
private int Median3<T>(T[] a, int i, int j, int k) where T : IComparable<T>
{
return
(Less(a[i], a[j]) ?
(Less(a[j], a[k]) ? j : Less(a[i], a[k]) ? k : i) :
(Less(a[k], a[j]) ? j : Less(a[k], a[i]) ? k : i));
}
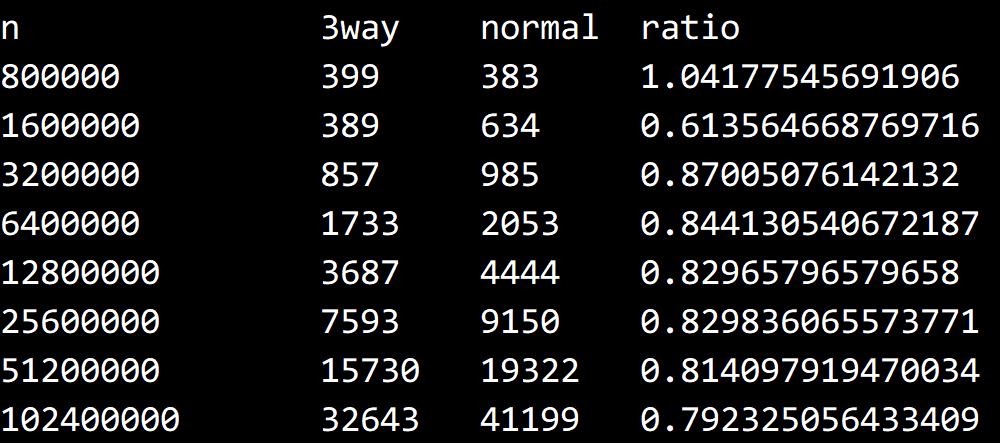
测试结果 #
提高约 20% 左右的性能。
代码 #
QuickBentleyMcIlroy
/// <summary>
/// 利用 Bentley-McIlroy 方法优化的快速排序。
/// </summary>
public class QuickBentleyMcIlroy : BaseSort
{
/// <summary>
/// 小于这个数值的数组调用插入排序。
/// </summary>
private readonly int _insertionSortCutoff = 8;
/// <summary>
/// 小于这个数值的数组调用中位数作为枢轴。
/// </summary>
private readonly int _medianOf3Cutoff = 40;
/// <summary>
/// 用快速排序对数组 a 进行升序排序。
/// </summary>
/// <typeparam name="T">需要排序的类型。</typeparam>
/// <param name="a">需要排序的数组。</param>
public override void Sort<T>(T[] a)
{
Sort(a, 0, a.Length - 1);
Debug.Assert(IsSorted(a));
}
/// <summary>
/// 对指定范围内的数组进行排序。
/// </summary>
/// <typeparam name="T">需要排序的类型。</typeparam>
/// <param name="a">需要排序的数组。</param>
/// <param name="lo">排序的起始下标。</param>
/// <param name="hi">排序的终止下标。</param>
private void Sort<T>(T[] a, int lo, int hi) where T : IComparable<T>
{
var n = hi - lo + 1;
if (n <= _insertionSortCutoff)
{
InsertionSort(a, lo, hi);
return;
}
if (n <= _medianOf3Cutoff)
{
// 对于较小的数组,直接选择左中右三个元素中的中位数作为枢轴。
var m = Median3(a, lo, lo + n / 2, hi);
Exch(a, m, lo);
}
else
{
// 对于较大的数组使用 Turkey Ninther 作为枢轴。
var eps = n / 8;
var mid = lo + n / 2;
var m1 = Median3(a, lo, lo + eps, lo + eps + eps);
var m2 = Median3(a, mid - eps, mid, mid + eps);
var m3 = Median3(a, hi - eps - eps, hi - eps, hi);
var ninther = Median3(a, m1, m2, m3);
Exch(a, ninther, lo);
}
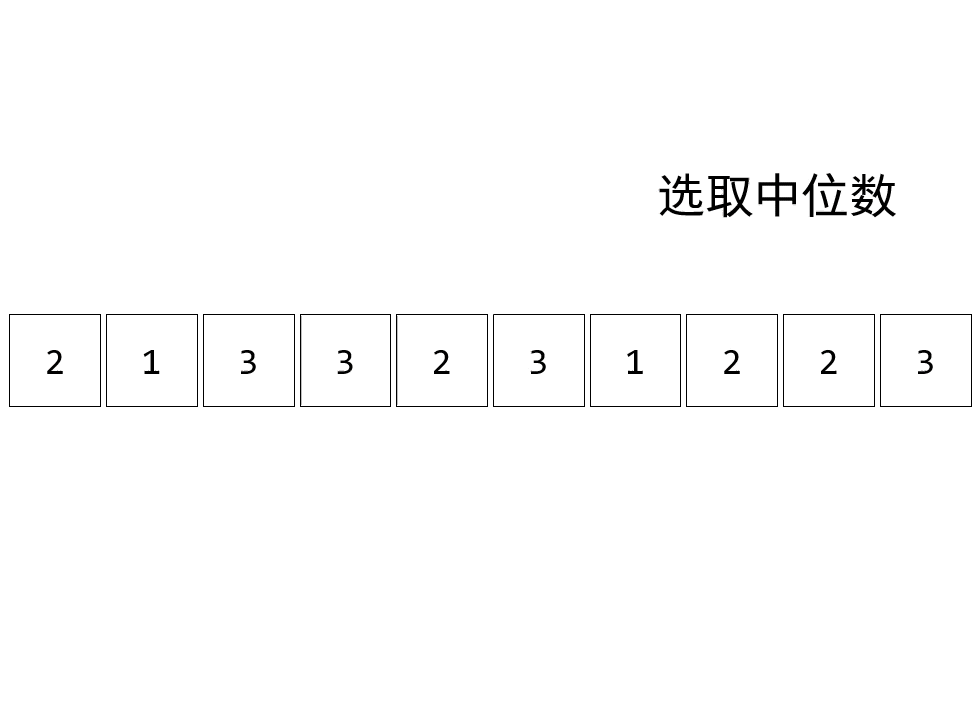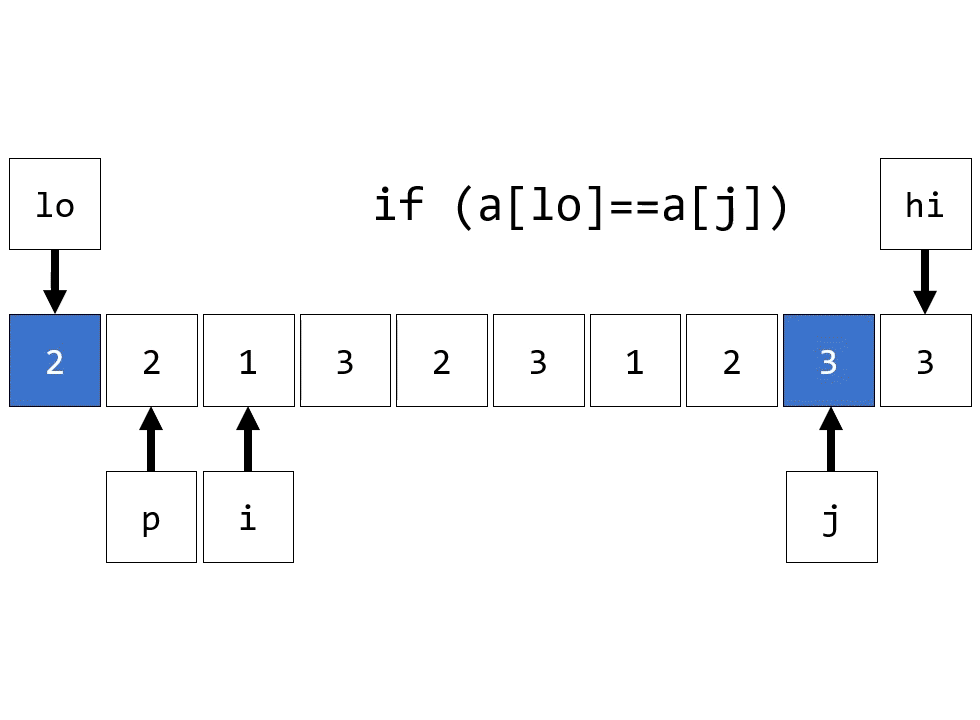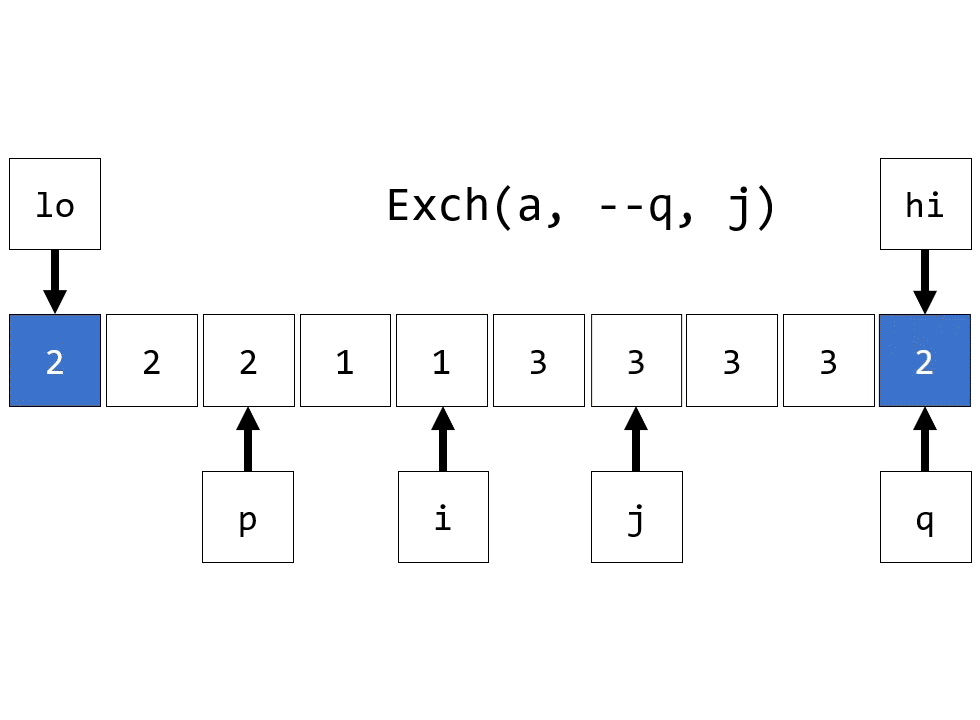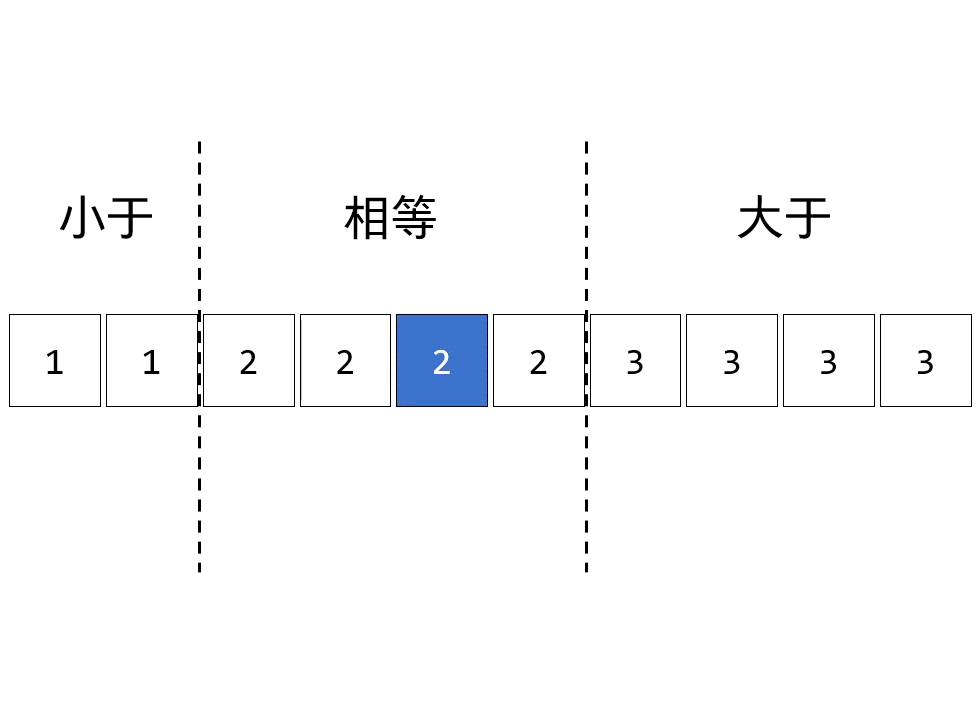
// 三向切分
int i = lo, j = hi + 1;
int p = lo, q = hi + 1;
var v = a[lo];
while (true)
{
while (Less(a[++i], v)) if (i == hi) break;
while (Less(v, a[--j]));
if (i == j && IsEqual(a[i], v))
Exch(a, ++p, i);
if (i >= j)
break;
Exch(a, i, j);
if (IsEqual(a[i], v))
Exch(a, ++p, i);
if (IsEqual(a[j], v))
Exch(a, --q, j);
}
i = j + 1;
for (var k = lo; k <= p; k++)
Exch(a, k, j--);
for (var k = hi; k >= q; k--)
Exch(a, k, i++);
Sort(a, lo, j);
Sort(a, i, hi);
}
/// <summary>
/// 判断两个元素是否值相等。
/// </summary>
/// <typeparam name="T">需要判断的元素类型。</typeparam>
/// <param name="a">进行比较的第一个元素。</param>
/// <param name="b">进行比较的第二个元素。</param>
/// <returns>两个元素的值是否相等。</returns>
private bool IsEqual<T>(T a, T b) where T : IComparable<T>
{
return a.CompareTo(b) == 0;
}
/// <summary>
/// 用插入排序对指定范围内的数组排序。
/// </summary>
/// <typeparam name="T">数组的元素类型。</typeparam>
/// <param name="a">需要排序的数组。</param>
/// <param name="lo">排序的起始下标。</param>
/// <param name="hi">排序的终止下标。</param>
private void InsertionSort<T>(T[] a, int lo, int hi) where T : IComparable<T>
{
for (var i = lo; i <= hi; i++)
{
for (var j = i; j > lo && Less(a[j], a[j - 1]); j--)
{
Exch(a, j, j - 1);
}
}
}
/// <summary>
/// 获取三个元素中的中位数。
/// </summary>
/// <typeparam name="T">用于排序的元素。</typeparam>
/// <param name="a">需要排序的数组。</param>
/// <param name="i">第一个待选元素的下标。</param>
/// <param name="j">第二个待选元素的下标。</param>
/// <param name="k">第三个待选元素的下标。</param>
/// <returns>下标为 <paramref name="i"/>,<paramref name="j"/>,<paramref name="k"/> 的元素中的中位数下标。</returns>
private int Median3<T>(T[] a, int i, int j, int k) where T : IComparable<T>
{
return
(Less(a[i], a[j]) ?
(Less(a[j], a[k]) ? j : Less(a[i], a[k]) ? k : i) :
(Less(a[k], a[j]) ? j : Less(a[k], a[i]) ? k : i));
}
}
测试用例
var quickNormal = new QuickSort();
var quickBentleyMcIlroy = new QuickBentleyMcIlroy();
var arraySize = 800000; // 初始数组大小。
const int trialTimes = 1; // 每次实验的重复次数。
const int trialLevel = 8; // 双倍递增的次数。
Console.WriteLine("n\t\t3way\tnormal\tratio");
for (var i = 0; i < trialLevel; i++)
{
double timeBentleyMcIlroy = 0;
double timeNormal = 0;
for (var j = 0; j < trialTimes; j++)
{
var a = SortCompare.GetRandomArrayInt(arraySize);
var b = new int[a.Length];
a.CopyTo(b, 0);
timeNormal += SortCompare.Time(quickNormal, b);
timeBentleyMcIlroy += SortCompare.Time(quickBentleyMcIlroy, a);
}
timeBentleyMcIlroy /= trialTimes;
timeNormal /= trialTimes;
if (arraySize < 10000000)
Console.WriteLine(
arraySize + "\t\t" + timeBentleyMcIlroy + "\t" + timeNormal + "\t" + timeBentleyMcIlroy / timeNormal);
else
Console.WriteLine(
arraySize + "\t" + timeBentleyMcIlroy + "\t" + timeNormal + "\t" + timeBentleyMcIlroy / timeNormal);
arraySize *= 2;
}
另请参阅 #
有关这种快速排序算法的来源以及三个数的中位数的选取算法,请参阅下面这篇 1993 年的论文: Bentley J L, McIlroy M D. Engineering a sort function[J]. Software: Practice and Experience, 1993, 23(11): 1249-1265.
下面这份 2002 年的 PPT 详细解释和分析了官方实现代码的思路和性能: Sedgewick R, Bentley J. Quicksort is optimal[J]. Knuthfest, Stanford University, Stanford, 2002.
有关选取中位数 Ninther 算法,请参阅下面这篇 1978 年的论文: Tukey J W. The ninther, a technique for low-effort robust (resistant) location in large samples[M]//Contributions to Survey Sampling and Applied Statistics. 1978: 251-257.
以及按照惯例给出本题用到的类库链接: Quick 库