2.3.18 #

解答 #

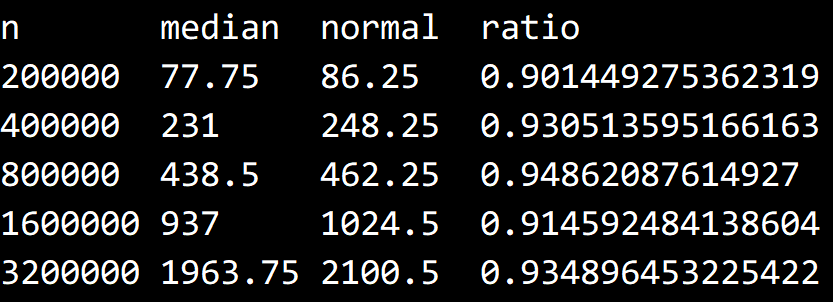
每次切分时都取前三个元素的中位数作为枢轴，这可以带来约 5%~10% 的性能提升。

这里通过三次比较将前三个数排序，然后把三个数中的中位数放到数组开头，最大值放到数组末尾。

最大值被放到了末尾，枢轴不可能大于末尾的这个数，因此右边界判断可以去掉。

同时由于枢轴不可能小于自身，因此左边界判断也可以去掉。

这样就可以把切分中的两个边界判断全部去掉了。

最后对于大小为 2 的数组做特殊处理，通过一次比较直接排序并返回。

测试结果：

代码 #

QuickSortMedian3 #

public class QuickSortMedian3 : BaseSort
{
    /// <summary>
    /// 用快速排序对数组 a 进行升序排序。
    /// </summary>
    /// <typeparam name="T">需要排序的类型。</typeparam>
    /// <param name="a">需要排序的数组。</param>
    public override void Sort<T>(T[] a)
    {
        Shuffle(a);
        Sort(a, 0, a.Length - 1);
        Debug.Assert(IsSorted(a));
    }

    /// <summary>
    /// 用快速排序对数组 a 的 lo ~ hi 范围排序。
    /// </summary>
    /// <typeparam name="T">需要排序的数组类型。</typeparam>
    /// <param name="a">需要排序的数组。</param>
    /// <param name="lo">排序范围的起始下标。</param>
    /// <param name="hi">排序范围的结束下标。</param>
    private void Sort<T>(T[] a, int lo, int hi) where T: IComparable<T>
    {
        if (hi <= lo)                   // 别越界
            return;

        // 只有两个元素的数组直接排序
        if (hi == lo + 1)
        {
            if (Less(a[hi], a[lo]))
                Exch(a, lo, hi);

            return;
        }

        var j = Partition(a, lo, hi);
        Sort(a, lo, j - 1);
        Sort(a, j + 1, hi);
    }

    /// <summary>
    /// 对数组进行切分，返回枢轴位置。
    /// </summary>
    /// <typeparam name="T">需要切分的数组类型。</typeparam>
    /// <param name="a">需要切分的数组。</param>
    /// <param name="lo">切分的起始点。</param>
    /// <param name="hi">切分的末尾点。</param>
    /// <returns>枢轴下标。</returns>
    private int Partition<T>(T[] a, int lo, int hi) where T : IComparable<T>
    {
        int i = lo, j = hi + 1;
            
        if (Less(a[lo + 1], a[lo]))
            Exch(a, lo + 1, lo);
        if (Less(a[lo + 2], a[lo]))
            Exch(a, lo + 2, lo);
        if (Less(a[lo + 2], a[lo + 1]))
            Exch(a, lo + 1, lo + 2);

        Exch(a, lo, lo + 1);        // 中位数放最左侧
        Exch(a, hi, lo + 2);        // 较大的值放最右侧作为哨兵

        var v = a[lo];
        while (true)
        {
            while (Less(a[++i], v))
            {
            }

            while (Less(v, a[--j]))
            {
            }

            if (i >= j)
                break;
            Exch(a, i, j);
        }
        Exch(a, lo, j);
        return j;
    }

    /// <summary>
    /// 打乱数组。
    /// </summary>
    /// <typeparam name="T">需要打乱的数组类型。</typeparam>
    /// <param name="a">需要打乱的数组。</param>
    private void Shuffle<T>(T[] a)
    {
        var random = new Random();
        for (var i = 0; i < a.Length; i++)
        {
            var r = i + random.Next(a.Length - i);
            var temp = a[i];
            a[i] = a[r];
            a[r] = temp;
        }
    }
}

测试用例 #

var quickNormal = new QuickSort();
var quickMedian = new QuickSortMedian3();
var arraySize = 200000; // 初始数组大小。
const int trialTimes = 4; // 每次实验的重复次数。
const int trialLevel = 5; // 双倍递增的次数。

Console.WriteLine("n\tmedian\tnormal\tratio");
for (var i = 0; i < trialLevel; i++)
{
    double timeMedian = 0;
    double timeNormal = 0;
    for (var j = 0; j < trialTimes; j++)
    {
        var a = SortCompare.GetRandomArrayInt(arraySize);
        var b = new int[a.Length];
        a.CopyTo(b, 0);
        timeNormal += SortCompare.Time(quickNormal, b);
        timeMedian += SortCompare.Time(quickMedian, a);

    }

    timeMedian /= trialTimes;
    timeNormal /= trialTimes;
    Console.WriteLine(arraySize + "\t" + timeMedian + "\t" + timeNormal + "\t" + timeMedian / timeNormal);
    arraySize *= 2;
}

另请参阅 #

Quick 库