2.2.25 #

解答 #

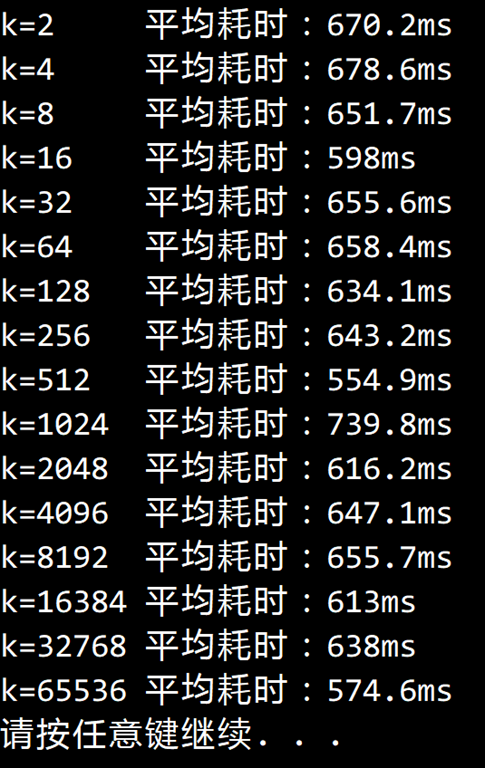
事实上 k 的取值无关紧要，实验也证明了这一点。

算法大致可以分为以下几个步骤首先将数组划为 k 份，

用一个数组 mids 记录这 k 个子数组的分割位置

随后递归的调用 Sort 方法，将这 k 个子数组排序随后将这 k 个子数组归并，

每次归并时遍历取 k 个子数组中值最小的一个，

然后对应子数组的指示器 + 1 上面这一步是 $O(k)$ 的，

可以用堆或者败者树优化为对数级别

代码 #

/// <summary>
/// k 路归并排序。
/// </summary>
public class MergeSortKWay : BaseSort
{
    /// <summary>
    /// 同时归并的数组数目。
    /// </summary>
    /// <value>同时归并的数组数目。</value>
    public int K { get; set; }

    /// <summary>
    /// 默认构造函数。
    /// </summary>
    public MergeSortKWay() { K = 2; }

    /// <summary>
    /// 用 k 向归并排序对数组 a 进行排序。
    /// </summary>
    /// <typeparam name="T"></typeparam>
    /// <param name="a"></param>
    /// <exception cref="ArgumentOutOfRangeException">数组长度小于 K 值时抛出异常。</exception>
    public override void Sort<T>(T[] a)
    {
        if (K > a.Length)
            throw new ArgumentOutOfRangeException(nameof(a), "数组长度不能小于 K 值！");

        var aux = new T[a.Length];
        Sort(a, aux, 0, a.Length - 1);
        Debug.Assert(IsSorted(a));
    }

    /// <summary>
    /// 自顶向下地对数组指定范围内进行 k 向归并排序，需要辅助数组。
    /// </summary>
    /// <typeparam name="T">需要排序的元素类型。</typeparam>
    /// <param name="a">原数组。</param>
    /// <param name="aux">辅助数组。</param>
    /// <param name="lo">排序范围起点。</param>
    /// <param name="hi">排序范围终点。</param>
    private void Sort<T>(T[] a, T[] aux, int lo, int hi) where T : IComparable<T>
    {
        if (hi <= lo)       // 小于或等于一个元素
            return;
        var mids = new int[K - 1];
        var steps = (hi - lo) / K;
        mids[0] = lo + steps;
        for (var i = 1; i < K - 1; i++)
        {
            mids[i] = mids[i - 1] + steps;
            if (mids[i] > hi)               // 防止溢出
                mids[i] = hi;
        }

        Sort(a, aux, lo, mids[0]);
        for (var i = 1; i < K - 1; i++)
        {
            Sort(a, aux, mids[i - 1] + 1, mids[i]);
        }
        Sort(a, aux, mids[K - 2] + 1, hi);
        Merge(a, aux, lo, mids, hi);
    }

    /// <summary>
    /// 将指定范围内的元素归并。
    /// </summary>
    /// <typeparam name="T">数组元素类型。</typeparam>
    /// <param name="a">原数组。</param>
    /// <param name="aux">辅助数组。</param>
    /// <param name="lo">范围起点。</param>
    /// <param name="mids">范围中间点。</param>
    /// <param name="hi">范围终点。</param>
    private void Merge<T>(T[] a, T[] aux, int lo, int[] mids, int hi) where T : IComparable<T>
    {
        for (var l = lo; l <= hi; l++)
        {
            aux[l] = a[l];
        }

        var pointers = new int[K]; // 标记每个数组的当前归并位置
        pointers[0] = lo;                 // 开始时归并位置处于每个子数组的起始
        for (var i = 1; i < K; i++)
        {
            pointers[i] = mids[i - 1] + 1;
        }
        // 开始归并
        for (var i = lo; i <= hi; i++)
        {
            // 找到最小值
            T min;
            var minPointerIndex = 0;
            var isInit = true;
            if (pointers[K - 1] > hi)
            {
                min = default;                 // 初始化以避免编译错误
            }
            else
            {
                min = aux[pointers[K - 1]];
                minPointerIndex = K - 1;
                isInit = false;
            }

            for (var j = 0; j < K - 1; j++)
            {
                if (pointers[j] > mids[j])      // 当前数组已经用完
                    continue;
                if (isInit)                     // 第一次赋值
                {
                    isInit = false;
                    min = aux[pointers[j]];
                    minPointerIndex = j;
                    continue;
                }
                if (Less(aux[pointers[j]], min))
                {
                    min = aux[pointers[j]];
                    minPointerIndex = j;
                }
            }

            // 将最小值赋给归并数组，对应子数组的归并位置+1
            a[i] = min;
            pointers[minPointerIndex]++;
        }
    }
}

另请参阅 #

Merge 库