2.2.13 #
解答 #
假设对三个数进行排序,
这三个数是:35,10,17
三个数排序的决策树如下,
结点代表比较对应位置上的数。
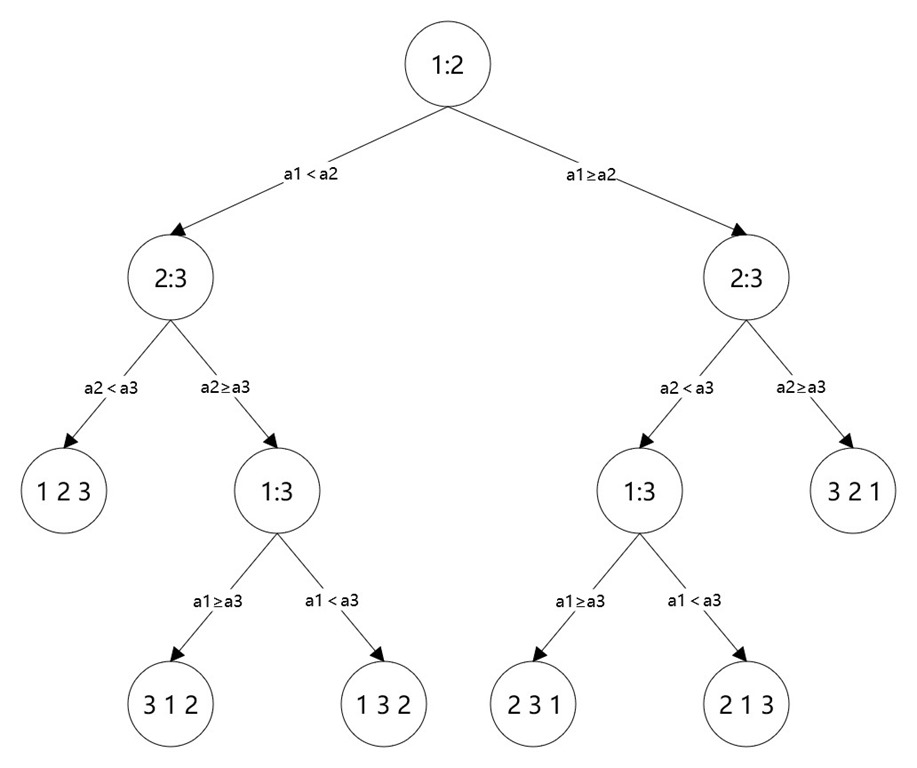
对于 35,10,17 来说,路径遵循右、左、左,最后得到的结果就是 2 3 1(10,17,35)。
我们可以发现决策树上的每一个叶子节点都代表一种排列顺序,对于 N 个数,叶子节点就有 $N!$ 个
根据二叉树的性质,高度为 $h$ 的二叉树最多有 $2^h$ 个叶子节点
那么,对于 $N$ 个数,决策树的高度 $h$ 的最小值可以通过下面这个式子得出来
$2^h >= n!$
$h \ge log(n!)$
因此可以得到决策树高度 $h$ 的最小值是 $log(n!)$
接下来我们来计算平均路径长度
我们令函数 $H(k)$ 代表有 $k$ 个叶子节点的平衡决策树的所有路径长度之和
上例中 $H(6) = 2 + 2 + 3 + 3 + 3 + 3 = 16$
由于平衡决策树的性质,$H(k) = 2H(k / 2) + k$ (加上 $k$ 的原因:左右子树的高度比整个树的高度小 $1$,因此每条路径的长度都必须加 $1$,总共多加了 $k$ 次)
因此 $H(k) = klogk$
现在令 $k = n!$
$H(n!) = n!log(n!)$
由于每次排序时我们只经过某一条路径(上例中我们只经过了右、左、左这条路径)
而且每种路径的出现概率相等
因此平均比较次数应该为 $H(n!) / n! = log(n!) = nlog(n)$
证明完毕