1.5.15 #

解答 #

首先证明在最坏情况下加权 quick-union 算法生成的树中的每一层结点数均为二项式系数。

最坏情况下，每次 union 操作都是合并相同大小的树，如下图所示：

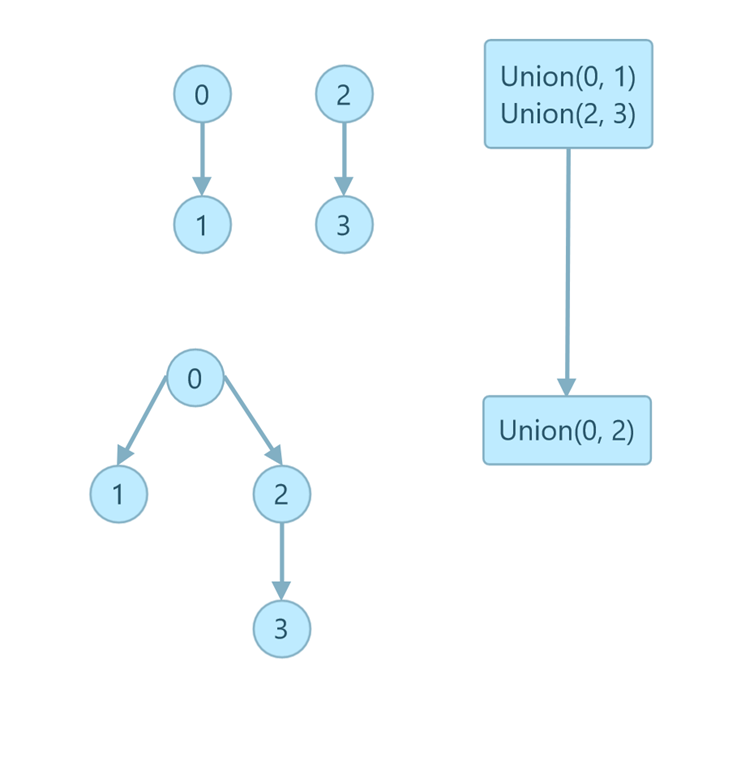
设第 i 层的结点数为 ki，那么最坏情况下每次合并后的 ki’ = ki + ki-1 。

这符合二项式系数的构造特点（详情可以搜索杨辉三角），

第一个结论证明完毕。

接下来求平均深度，首先根据二项式的求和公式，一棵深度为 n 的树（根结点的深度为零）结点总数为：

$$ \sum_{k=0}^{n} \begin{pmatrix} n \newline k \end{pmatrix} =2^n $$

每层结点数 × 该层深度后的和为：

$$ \sum_{k=0}^{n}k \cdot \begin{pmatrix} n \newline k \end{pmatrix}=n\sum_{k=1}^{n} \begin{pmatrix} n-1 \newline k-1 \end{pmatrix}=n\sum_{s=0}^{n-1} \begin{pmatrix} n-1 \newline s \end{pmatrix}=n2^{n-1} $$

这里用到了这个公式化简：

$$ \begin{pmatrix} n \newline k \end{pmatrix}=\frac{n}{k} \begin{pmatrix} n-1 \newline k-1 \end{pmatrix} $$

相除可以求得平均深度：

$$ \bar{D} = \frac{\sum_{k=0}^{n}k\cdot\begin{pmatrix}n\newline k\end{pmatrix}}{\sum_{k=0}^{n}\begin{pmatrix}n\newline k\end{pmatrix}}=\frac{n2^{n-1}}{2^n}=\frac{n}{2} $$